бое тело, погруженное в жидкость, подвергается сжимающему и выталкивающему действию со стороны жидкости.
Представим такую ситуацию: ученый, владеющий современными приборами и мощным математическим аппаратом, решил вычислить силу, выталкивающую из жидкости погруженное в нее тело.
Он экспериментально установит, что на единицу поверхности тела, погруженного в жидкость с плотностью действует по нормали к поверхности сила гидростатического давления p, зависящая от глубины погружения h по определенному закону (gh) и не зависящая от ориентации поверхности.
Он сложит векторы сил давления, действующих на различные элементы поверхности тела и направленные по нормали к ним; для этого потребуется вычислить так называемый поверхностный интеграл от некоторой векторной функции по поверхности тела сложной формы. С современного математического аппарата и мощных компьютеров этот интеграл может быть вычислен. Но каково же будет изумление
Рассмотрим общий случай. Тело подвешено на пружине и находится в состоянии покоя. На тело действует сила тяжести и сила упругости. Оно в покое, поэтому ускорение а=0
Второй закон Ньютона можем записать в следующем виде
- это векторная запись.
Сила тяжести mg, а сила упругости kΔx. Тк силы разнонаправлены, и учитываем состояние покоя получаем
mg - kΔx = 0 mg = kΔx
учитываем, что 450 г = 0,45 кг, а при расчете g берем 10
Δx =
Получаем, что пружина отклонилась на 6 см.
Аналогично подставляем в формулы 2m и 3m. Получаем, что в случае 2 это будет 12 см, а в 3 - 18 см.
Найдем силы:
F₁= 0.06*75 = 4.5 Н
F₂= 0.12*75 = 9 Н
F₃= 0.18*75 = 13.5 Н
В прикрепленных файлах: схема эксперимента и построенные графики.
бое тело, погруженное в жидкость, подвергается сжимающему и выталкивающему действию со стороны жидкости.
Представим такую ситуацию: ученый, владеющий современными приборами и мощным математическим аппаратом, решил вычислить силу, выталкивающую из жидкости погруженное в нее тело.
Он экспериментально установит, что на единицу поверхности тела, погруженного в жидкость с плотностью действует по нормали к поверхности сила гидростатического давления p, зависящая от глубины погружения h по определенному закону (gh) и не зависящая от ориентации поверхности.
Он сложит векторы сил давления, действующих на различные элементы поверхности тела и направленные по нормали к ним; для этого потребуется вычислить так называемый поверхностный интеграл от некоторой векторной функции по поверхности тела сложной формы. С современного математического аппарата и мощных компьютеров этот интеграл может быть вычислен. Но каково же будет изумление
Объяснение:
Объяснение:
Рассмотрим общий случай. Тело подвешено на пружине и находится в состоянии покоя. На тело действует сила тяжести и сила упругости. Оно в покое, поэтому ускорение а=0
Второй закон Ньютона можем записать в следующем виде
Сила тяжести mg, а сила упругости kΔx. Тк силы разнонаправлены, и учитываем состояние покоя получаем
mg - kΔx = 0 mg = kΔx
учитываем, что 450 г = 0,45 кг, а при расчете g берем 10
Δx =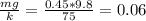
Получаем, что пружина отклонилась на 6 см.
Аналогично подставляем в формулы 2m и 3m. Получаем, что в случае 2 это будет 12 см, а в 3 - 18 см.
Найдем силы:
F₁= 0.06*75 = 4.5 Н
F₂= 0.12*75 = 9 Н
F₃= 0.18*75 = 13.5 Н
В прикрепленных файлах: схема эксперимента и построенные графики.