Линейной скоростью называется скорость, с которой точка движется по окружности.
Формулу для величины линейной скорости можно вывести на основании следующих рассуждений. Точка, лежащая на окружности радиуса R, за один оборот пройдёт путь, равный длине окружности 2πR, за время, равное периоду Т. Взяв отношение пути 2πR ко времени T, мы получим скорость движения точки по окружности:
Решение проводим в Солнечной системе, поскольку нам необходимы характеристики центрального звёздного тела, а они явно не заданы, из чего следовательно проистекает вывод, что по-умолчанию, вопрос задаётся в Солнечной системе.
Синодический период T' характеризует период обращения планеты относительно Земли.
С ним связана синодическая угловая скорость: |ω'| = 2π/Tn относительно Земли.
ω' = ±2π/Tn ;
Угловая скорость Земли: ω = 2π/T, где T = год = 365.2423 суток.
Ясно что синодическая угловая скорость планеты (относительно Земли) выражается как:
ω' = ωo – ω , где ωo = 2π/To – сидерические (собственные) угловая скорость и период планеты;
Линейной скоростью называется скорость, с которой точка движется по окружности.
Формулу для величины линейной скорости можно вывести на основании следующих рассуждений. Точка, лежащая на окружности радиуса R, за один оборот пройдёт путь, равный длине окружности 2πR, за время, равное периоду Т. Взяв отношение пути 2πR ко времени T, мы получим скорость движения точки по окружности:
Так как 1/T = n, где n - число оборотов, то: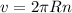
Учитывая ω = 2πn, получим: v = ωR
Синодический период T' характеризует период обращения планеты относительно Земли.
С ним связана синодическая угловая скорость: |ω'| = 2π/Tn относительно Земли.
ω' = ±2π/Tn ;
Угловая скорость Земли: ω = 2π/T, где T = год = 365.2423 суток.
Ясно что синодическая угловая скорость планеты (относительно Земли) выражается как:
ω' = ωo – ω , где ωo = 2π/To – сидерические (собственные)
угловая скорость и период планеты;
±2π/T' = 2π/To – 2π/T ;
1/T' = 1/To – 1/T , или 1/T' = 1/T – 1/To , откуда:
1/To = 1/T ± 1/T' ;
To = 1/[1/T±1/T'] ;
По закону Кеплера:
(To/T)² = (Bo/B)³ ,
где B и Bo – большие полуоси Земли и планеты соответственно;
Bo = B ³√[To²/T²] ;
To/T = 1/[1±T/T'] ;
Bo = B / ³√[(1±T/T')²] ;
Bo = B / ³√[(1±T/T')²] ≈ 150 млн.км / ³√[(1±365.2423/500)²] ;
Bo[1] ≈ 359 млн.км ;
наиболее близко к Церере ( B = 414 млн.км, Син. период ≈ 467 дней ) ;
Bo[2] ≈ 104 млн.км ;
наиболее близко к Венере ( B = 108 млн.км, Син. период ≈ 584 дней ).