фокусник Гарри Гудини уронил свою цилиндрическую шляпу массой 500 г и высотой 10 см и площадью 1 квадратный дециметр в цилиндрическую бочку высотой 250 см и площадью дна 10 квадратных дециметров заполненную водой шляпа не касается стенок бочки не намокает не протекает донышко шляпы горизонтально вода из бочки не выливается плотность воды 1Г на квадратных сантиметрах Как изменится уровень воды в бочке Будет ли плавать шляпа или утонет На сколько миллиметров шляпа погрузиться в воду ответ округлить до целых На сколько миллиметров изменился уровень воды в бочке после того как в неё попала шляпа

Объяснение:

S = v*t

До встречи в 12:00 .

После встречи тоже S1=v1*t1

v1=90км*ч

t1=32 минуты = 8/15 часа(легковая)

После встречи для грузового S2=v2*t2

t2(для грузового) = 50 минут=5/6 часа

S1=S2(легковая из Жодино в Минск ,грузовая из Минска в Жодино ) .

Тогда v1*t1=v2*t2

v*t=v*5/6

v*8/15=v*t

Так расстояние пройденное легковым с какой-то скоростью и за какое-то время равняется расстоянию ,пройденное грузовым с какой-то скоростью и за какое-то время .

t²=4/9

Пишем это всё под корнем :

²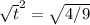

Отсюда :

t=2/3

v = 2/3 : 5/6 * 90 = 72 км/ч

Дано:

S = (1/4)s

t = 3 c

g = 10 м/с²

t_o, υ_0 - ?

Начальную скорость выразим из формулы, взяв полное время подъёма:

υ = υ_0 - g*t_o

Т.к. в верхней точке подъёма υ = 0, то

υ_0 = g*t_o

Теперь составим уравнение для полного пути, используя формулу перемещения:

s = υ_0*t_o - g*t_o²/2

Подставим вместо υ_0 его выражение:

s = g*t_o*t_o - g*t_o²/2 = g*t_o²*(1 - 1/2) = g*t_o²/2

Теперь, если разделить обе части уравнения на 4, получим следующее:

s/4 = (g*t_o²/2)/4

(1/4)s = g*t_o²/8

Тогда составим уравнение для последней 1/4 перемещения. Но сначала выразим начальную скорость υ_0', которой тело обладало через время t' = t_o - t:

υ_0' = υ_0 - g*(t_o - t) =>

(1/4)s = υ_0'*t - g*t²/2 = (υ_0 - g*(t_o - t))*t - g*t²/2

Учитывая, что υ_0 = g*t_o, получаем:

(1/4)s = (g*t_o - g*t_o + g*t)*t - g*t²/2 = g*t² - g*t²/2 = g*t*(1 - 1/2) = g*t²/2

Приравниваем оба выражения (1/4)s:

g*t²/2 = g*t_o²/8 | : (g/2)

t² = t_o²/4 => t_o² = 4*t² => t_o = √(4*t²) = 2*t = 2*3 = 6 c

Значит начальная скорость равна:

υ_0 = g*t_o = 10*6 = 60 м/с