:Измерения поверхностного натяжения жидкости . Осталось посчитать по формулам . Мне очень нужно надеюсь на Вас

:Измерения поверхностного натяжения жидкости . Осталось посчитать по формулам . Мне очень нужно на

Показать ответ

Ответ:

mishka1113

28.12.2021 03:45

Дано:

Начальная скорость: V₀ = 36 км/ч = 10 м/с.

Ускорение: a = 0,2 м/с².

"Начало" 10-ой секунды: t₁ = 9 c.

"Конец" 10-ой секунды: t₂ = 10 c.

Время для второй части задачи: t = 10 c.

Найти нужно путь за десятую секунду S - ? и мгновенную скорость V - ?

Решение:

1. Формула пути равноускоренного движения: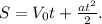 $S = V_0t + \frac{at^2}{2}.$

2. Путь за 9 секунд движения: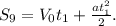 $S_9 = V_0t_1 + \frac{at_1^2}{2}.$

3. Путь за 10 секунд движения: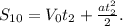 $S_{10} = V_0t_2 + \frac{at_2^2}{2}.$

4. Путь за десятую секунду - разность пути за десять секунд движения и пути за девять:

$S = S_{10} - S_9 = (V_0t_2 + \frac{at_2^2}{2}) - (V_0t_1 + \frac{at_1^2}{2}) = V_0(t_2 - t_1) + \frac{a}{2}(t_2^2 - t_1^2).$

5. Формула мгновенной скорости в момент времени: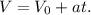 V = V_0 + at.

Численно получим: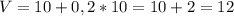

$S = 10*(10 - 9) + \frac{0,2}{2}(10^2 - 9^2) = 10 + 0,1(100 - 81) = 10 + 1,9 = 11,9$ (м).

V = 10 + 0,2 * 10 = 10 + 2 = 12 (м/с).

ответ: 11,9 м; 12 м/с.

0,0(0 оценок)

Ответ:

MstyanKristina

01.12.2022 11:12

А) Если конденсатор сначала заряжают, а затем отключают от источника напряжения, то неизменным остается заряд q на обкладках, а при увеличении втрое расстояния изменяется емкость С и напряжение U на нем. Соответственно энергия W=q^2/2C. Так как емкость С=eS/d, C1=eS/d, C2=eS/3d =C1/3, то W2=3W1.
б) Если конденсатор остается подключенным, то у такого конденсатора изменяется вследствие увеличении расстояния его емкость С2=C1/3 и заряд на обкладках q=C*U. U естественно остается тем же, а q2=C2*U=C1*U/3.
W2=q2^2/2C2=3(C1*U)^2/9*2*C1=(C1*U)^2/6*C1=C*U^2/6=W1/3, W1=C*U^2/2.

0,0(0 оценок)

Популярные вопросы: Физика