Известно, что площадь малого поршня равна 192 см2, а большого — 576 см2. Вес шара равен 143 Н. Найди вес груза, находящегося на поршне с большей площадью, если жидкость в гидравлической машине находится в равновесии.
Пусть для определенности и слово говорит человек, стоящий в точке A (см. рисунок)
1) Напрямую звук пойдёт по зеленому пути AB, его длина по условию l. Тогда если длительность звучания слова t, то конец слова второй услышит через время .
2) Эхо распространится вдоль красного пути AXB, это кратчайший путь, соединяющий A и B, касающийся стенки. Его можно представлять как кратчайший путь от воображаемого человека, который стоит за стеной на таком же расстоянии, что и первый, в точке . Длину этого пути найдём по теореме Пифагора.
- Расстояние вдоль стены между людьми находим из маленького треугольника сверху:
Пусть плотность первой жидкости , второй жидкости , а шара , тогда запишем общий объём шара
Найдем объем шара находящийся над водой, для этого общий объем разделим на 4 (по условию), и получим (1)
Повторим для нижней части шара, только умножим на 3/4, так как логично, что оставшаяся часть шара под разделом жидкостей, и получим (2)
Чтобы найти массы этих частей шара, надо найденный объем умножить на плотность шара:
(3)
(4)
Работа с формулами и уравнением:
На шар действуют 2 силы: Архимеда и тяжести, так как шар неподвижен, то сила действующая на обе части "вниз", равна силе действующей на обе части "вверх", запишем общий вид:
Подставим объем и массы из пунктов (1-4) и сократим на и на , в итоге останется:
Объяснение:
Пусть для определенности и слово говорит человек, стоящий в точке A (см. рисунок)
и слово говорит человек, стоящий в точке A (см. рисунок)
1) Напрямую звук пойдёт по зеленому пути AB, его длина по условию l. Тогда если длительность звучания слова t, то конец слова второй услышит через время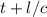 .
.
2) Эхо распространится вдоль красного пути AXB, это кратчайший путь, соединяющий A и B, касающийся стенки. Его можно представлять как кратчайший путь от воображаемого человека, который стоит за стеной на таком же расстоянии, что и первый, в точке . Длину этого пути найдём по теореме Пифагора.
. Длину этого пути найдём по теореме Пифагора.
- Расстояние вдоль стены между людьми находим из маленького треугольника сверху:
вдоль стены между людьми находим из маленького треугольника сверху:
- Длину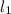 отрезка
отрезка  — из треугольника
— из треугольника  :
:
Начало слова второй услышимт через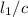
Тогда
Введение и выражение величин:
Пусть плотность первой жидкости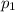 , второй жидкости
, второй жидкости 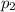 , а шара
, а шара 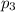 , тогда запишем общий объём шара
, тогда запишем общий объём шара 
Найдем объем шара находящийся над водой, для этого общий объем разделим на 4 (по условию), и получим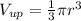 (1)
(1)
Повторим для нижней части шара, только умножим на 3/4, так как логично, что оставшаяся часть шара под разделом жидкостей, и получим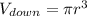 (2)
(2)
Чтобы найти массы этих частей шара, надо найденный объем умножить на плотность шара:
Работа с формулами и уравнением:
На шар действуют 2 силы: Архимеда и тяжести, так как шар неподвижен, то сила действующая на обе части "вниз", равна силе действующей на обе части "вверх", запишем общий вид:
Подставим объем и массы из пунктов (1-4) и сократим на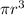 и на
и на 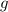 , в итоге останется:
, в итоге останется:
Подставим значения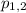 и решим уравнение:
и решим уравнение:
Получим те самые циферки из ответа