К коромыслу весов подвешены два гранитных цилиндра одинакового объёма.
Подумай, нарушится ли равновесие весов, если один цилиндр окажется в бензине, а другой — в морской воде.

Заполни окошки.

Плотность морской воды , чем плотность бензина.
Сила Архимеда, действующая на цилиндр в морской воде, , чем в бензине.

Сделай вывод.
ЧТО ВЕРНО? Равновесие весов не нарушится.
Равновесие весов нарушится.

Показать ответ

Ответ:

matveiruzkovjoping56

06.11.2021 10:45

)

Решим через теорему о центре масс:

В начале, в декартовой системе координат на плоскости рисунка(оси x и y направим так, что центр диска имеет координаты (R;R)) определим расположение центра масс, очевидно - что он в центре

Масса M1+M2+M3+M4+M = 1000 кг

После того как мальчишки разошлись, найдем x(ц.масс) и (у.цмаа) относительно льда, понимая, что система в целом изменила свои позиции

x(системы) =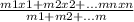 $\frac{m1x1+m2x2+...mnxn}{m1+m2+...m}$ , (аналогично и y) =>

x(системы) = ((80+750+50)*R+80*2R)/1000 = 1.04R

y(системы) = ((40+750+80)*R+50*2R)/1000 = 0.97R

По формуле расстояние между двумя точками на плоскости

$S = \sqrt{(x1-x2)^{2} +(y1-y2)^{2} }$

$S = \sqrt{((R-0.97R))^{2} +((R-1.04R))^{2}} = \sqrt{0.03R^{2} + 0.04R^{2} } = 0.05R$

0.05R = 0.05*1000 = 50 см

ответ: 50 cm

0,0(0 оценок)

Ответ:

margarita030620

07.08.2020 22:47

Дано:

X = A*sin(ωt)

Y = A*(1 - cos(ωt))

A = 1,5 см

ω = 0,5 с^-1

t = 5 c

s - ?

Если подставить в уравнения координат начальный момент времени t = 0, то получим начальное положение точки:

Х = А*sin(ω*0) = A*sin(0) = 0

Y = A*(1 - cos(ω*0)) = A*(1 - cos(0)) = A*(1 - 1) = 0

Значит, точка находилась в начале системы координат. Очевидно, что при заданных уравнениях координат движение точки раскладывается на колебательное вдоль оси Х и такое же - вдоль оси Y. Полное движение - вращательное. Также очевидно то, что через 5 секунд точка не будет находится на какой-то из осей координатной системы, т.к. Х и Y будут больше нуля. Точка будет над осью Х и справа от оси Y. Следовательно, перемещение мы можем найти по правилу Пифагора - им будет являться гипотенуза прямоугольного треугольника, в котором катетами являются отрезки, отложенные от начала системы координат. Длины отрезков равны значению координат X и Y в момент времени t = 5 c.

с² = а² + b²

s² = X² + Y² = A²*sin²(ω*t) + A²*(1 - cos(ω*t))² = A²*(sin²(ω*t) + 1 - 2*cos(ω*t) + cos²(ω*t)) = A²*(1 + 1 - 2*cos(ω*t)) = A²*2*(1 - cos(ω*t)) =>

=> s = A*√(2*(1 - cos(ω*t))) = 1,5*√(2*(1 - cos(0,5*5))) = 1,5*√(2*(1 - cos(2,5))) = 1,5*√2*(1 - (-0,8))) = 1,5*√(2*1,8) = 2,8460... = 2,8 см

ответ: 2,8 см.