эффективный диаметр молекулы — минимальное расстояние, на которое сближаются центры двух молекул при столкновении.
при столкновении, молекулы сближаются до некоторого наименьшего расстояния, которое условно считается суммой радиусов взаимодействующих молекул. столкновение между одинаковыми молекулами может произойти только в том случае, если их центры сблизятся на расстояние, меньшее или равное диаметру d - — эффективному диаметру молекулы.
через эффективный диаметр молекулы можно выразить эффективное сечение молекулы — как круг радиусом d. столкновение между молекулами возможно только в том случае, когда центр молекулы окажется внутри круга, представляющего собой эффективное сечение молекулы.
с точки зрения теории межмолекулярных взаимодействий эффективный радиус, представляющий собой половину эффективного диаметра — расстояние от условного центра молекулы, отвечающее минимуму потенциальной энергии в поле этой молекулы.
для молекул, имеющих точечную симметрию, условный центр может быть определен как центр масс молекулы, для сложных молекул он определяется феноменологически.
в общем случае эффективный радиус — усредненная величина, т.к. в случае, когда молекула не является концентрически симметричной (одноатомная молекула), радиус является функцией от угла в системе, связанной с молекулой.
Дано:
m = 100 гр = 0,1 кг
k = 0,5 кН/м = 500 Н/м
A = 20 см = 0,2 м
-------------------------------------
Найти:
E - ? υ(max) - ?
Запишем формулы кинетической энергий и потенциальной энергий тела при деформированной пружины:
Теперь мы используем закон сохранения механической энергий:
Максимальное отклонение равно амплитуде колебания, скорость в этом энергий равно нулю, давайте запишем:
Пусть υ = 0, тогда:
Пусть x = A, следовательно: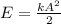
- Общая формула сохранения механической энергий.
E = 500 Н/м × (0,2 м)²/2 = 500 Н/м × 0,04 м²/2 = 20 Н×м/2 = 10 Н×м = 10 Дж
Максимальная скорость достигается в положений равновесия, при этом его отклонение равно нулю:
Пусть x = 0, тогда: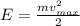
, следовательно мы получим:
υ(max) = 0,2 м × √500 Н/м/0,1 кг = 0,2 м × √500 кг×м/с²/м / 0,1 кг = 0,2 м × √500 кг/с²/0,1 кг = 0,2 м × √5000 1/с² = 0,2 м × √5000 с⁻² ≈ 0,2 м × 70,71 с⁻¹ ≈ 14,142 м/с ≈ 14,14 м/с
ответ: E = 10 Дж, υ(max) = 14,14 м/с
объяснение:
эффективный диаметр молекулы — минимальное расстояние, на которое сближаются центры двух молекул при столкновении.
при столкновении, молекулы сближаются до некоторого наименьшего расстояния, которое условно считается суммой радиусов взаимодействующих молекул. столкновение между одинаковыми молекулами может произойти только в том случае, если их центры сблизятся на расстояние, меньшее или равное диаметру d - — эффективному диаметру молекулы.
через эффективный диаметр молекулы можно выразить эффективное сечение молекулы — как круг радиусом d. столкновение между молекулами возможно только в том случае, когда центр молекулы окажется внутри круга, представляющего собой эффективное сечение молекулы.
с точки зрения теории межмолекулярных взаимодействий эффективный радиус, представляющий собой половину эффективного диаметра — расстояние от условного центра молекулы, отвечающее минимуму потенциальной энергии в поле этой молекулы.
для молекул, имеющих точечную симметрию, условный центр может быть определен как центр масс молекулы, для сложных молекул он определяется феноменологически.
в общем случае эффективный радиус — усредненная величина, т.к. в случае, когда молекула не является концентрически симметричной (одноатомная молекула), радиус является функцией от угла в системе, связанной с молекулой.
= (∫∫r(φ,θ)d×φ×d×θ)/2π²