Кулька, що летіла зі швидкістю 20 м/с, після лобового пружного зіткнення з нерухомим кубом продовжила рухатись в тому самому напрямку зі швидкістю 10 м/с. визначте у скільки разів маса кульки більша за масу куба.

Показать ответ

Ответ:

taibat3

10.06.2022 00:30

Сдвинем всю картинку так, чтобы начальная точка оказалась в начале координат. Это ни на что не влияет. Дальше под координатами я буду понимать сразу сдвинутые координаты.

Известно, что траектория (если не учитывать сопротивление воздуха и прочие прелести реальной жизни) параболическая. Забудем о физике и найдём уравнения траекторий, проходящих через начало координат и заданную точку.

$y_n=-a x_n^2+b x_n\\b=\dfrac{y_n+ax_n^2}{x_n}$

Парабола выпукла вверх, поэтому чтобы вся она была выше какого-то отрезка, достаточно проверить концы этого отрезка. Условие того, что парабола выше какой-то точки:

$-ax_i^2+bx_i\geqslant y_i$

Подставляем значение b и получается линейное неравенство:

$ax_i(x_n-x_i)\geqslant y_i-y_n\cdot\dfrac{x_i}{x_n}\\a\geqslant \dfrac{{y_i}/x_i-y_n/x_n}{x_n-x_i}$

Выписываем такие неравенство для всех точек, решение имеет вид

$a\geqslant\max\limits_{i1}\left(\dfrac{{y_i}/x_i-y_n/x_n}{x_n-x_i}\right)=a^*$

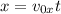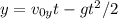Подставив t из $x=v_{0x}t$ в $y=v_{0y}t-gt^2/2$ , получаем, что

$y(t)=-at^2+bt=-\dfrac{g}{2v_{0x}^2}t^2+\dfrac{v_{0y}}{v_{0x}}t$

Выражаем компоненты начальной скорости:

$v_{0x}^2=\dfrac g{2a}\\v_{0y}^2=b^2v_{0x}^2=\dfrac g{2a}\cdot\left(ax_n+\dfrac{y_n}{x_n}\right)^2$

Квадрат начальной скорости равен

$v_0^2=v_{0x}^2+v_{0y}^2=\dfrac g{2a}+\dfrac g{2a}\cdot\left(ax_n+\dfrac{y_n}{x_n}\right)^2$

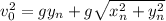Его нужно минимизировать. Это можно сделать при производной или численно. Производная даст ответ, что минимальное значение $v_0^2=gy_n+g\sqrt{x_n^2+y_n^2}$ достигается при

$a^{**}=\dfrac{\sqrt{x_n^2+y_n^2}}{x_n^2}$ a

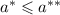Если $a^*\leqslant a^{**}$ , то ответ - корень из 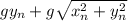$gy_n+g\sqrt{x_n^2+y_n^2}$ , иначе - корень из

$\dfrac g{2a^*}+\dfrac g{2a^*}\cdot\left(a^* x_n+\dfrac{y_n}{x_n}\right)^2$

0,0(0 оценок)

Ответ:

SHEVENIST

03.12.2022 18:04

Дано:
m = 100 г = 0.1 кг;
h=4R;
P - ?
Решение:
Запишем второй закон Ньютона для шарика при прохождении нижней точки траектории: N+mg+ma=0;
N - сила реакции опоры. Она противоположна по направлению и равна по модулю P: P=-N. Тогда mg+ma=-N; m(a+g)=P.

Массу шарика мы знаем, ускорение свободного падения равно 10 м/с². Остается найти центростремительное ускорение a.
a=V²/R.

По закону сохранения механической энергии, вся потенциальная энергия, которой обладал шар в момент, когда его отпустили, перейдет в кинетическую:
Ep=Ek;
mgh=mV²/2;
V²=2gh;
V²=8gR (т. к. h=4R по условию);
Значит a=V²/R=8gR/R=8g.

Осталось просто подставить наше найденное ускорение и посчитать)
P=m(a+g)=m(8g+g)=9mg=9*0.1*10=9 Н.
ответ: 9 Н.

0,0(0 оценок)

Популярные вопросы: Физика