Данные пробирки имеют одинаковую частоту вращения, но разные линейные скорости, так как одна пробирка находится дальше другой от центра центрифуги. Пусть r₁ = R – радиус окружности, описываемый первой пробиркой, тогда r₂ = (R - 11) – это радиус окружности, по какой движется вторая пробиркой. Циклические частоты пробирок одинаковы ⇒ ω₁ = ω₂, а линейные скорости по условию равны: v₁ = 56 м/с, v₂ = 34 м/с
По формуле из кинематики: v₁ = ω₁·r₁, v₂ = ω₂·r₂ ⇒ ω₁ = v₁/r₁ = ω₂ = v₂/r₂ ⇒ v₁/R = v₂/(R - 11) ⇒ (по правилу пропорции) v₁ · (R - 11) = v₂ · R ⇒
R · (v₁ - v₂) = 11 · v₁ ⇒ R = сантиметров
ответ: первая пробирка описывает окружность радиусом в 28 см.
Данные пробирки имеют одинаковую частоту вращения, но разные линейные скорости, так как одна пробирка находится дальше другой от центра центрифуги. Пусть r₁ = R – радиус окружности, описываемый первой пробиркой, тогда r₂ = (R - 11) – это радиус окружности, по какой движется вторая пробиркой. Циклические частоты пробирок одинаковы ⇒ ω₁ = ω₂, а линейные скорости по условию равны: v₁ = 56 м/с, v₂ = 34 м/с
По формуле из кинематики: v₁ = ω₁·r₁, v₂ = ω₂·r₂ ⇒ ω₁ = v₁/r₁ = ω₂ = v₂/r₂ ⇒ v₁/R = v₂/(R - 11) ⇒ (по правилу пропорции) v₁ · (R - 11) = v₂ · R ⇒
R · (v₁ - v₂) = 11 · v₁ ⇒ R =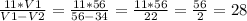 сантиметров
сантиметров
ответ: первая пробирка описывает окружность радиусом в 28 см.
Объяснение:
Дано:
a = 20 м/с²
L = 2 км = 2 000 м
t = 10 c
V₀ - ?
1)
За 10 секунд ракета поднимется на высоту:
H = a·t² / 2 = 20·10² / 2 = 1000 м
2)
Теперь запишем уравнения движения снаряда:
x = (V₀·cos α)·t
y = (V₀·sin α)·t - g·t² / 2
3)
Учтем, что
L = x
2 000 = (V₀·cos α)·10
V₀·cos α = 200 (1)
4)
Снаряд попадет в ракету, если:
H = y
H = (V₀·sin α)·t - g·t² / 2
1000 = (V₀·sin α)·10 - 10·10² / 2
100 = (V₀·sin α) - 50
V₀·sin α = 50 (2)
Разделим уравнение (2) на уравнение (1):
tg α = 50 / 200 = 0,25
Угол :
α ≈ 14°
Тогда из (2)
V₀ = 50 / sin α = 50 / sin 14° = 50 / 0,24 ≈ 210 м/с