Так как объемы тел одинаковые, то, поскольку равновесие весов не нарушилось, одинаковыми будут и моменты сил, действующих на эти тела при погружении в жидкости. Тогда:
Найдем d₁/d₂:
Так как до погружения в жидкость весы находились в равновесии, то:
M₁ = M₂ => m₁gd₁ = m₂gd₂ => d₁/d₂= ρ₀₂gV : ρ₀₁gV = ρ₀₂/ρ₀₁ =
= 6150 : 9800 ≈ 0,63
Так как плотность первой жидкости 790 кг/м³, то плотность второй:
ρ₂ = ρ₁ * d₁/d₂ = 790*0,63 = 496 (кг/м³)
ответ: 496 кг/м³
Смотрите мой "перевод" вашей задачи в комментариях к вопросу. Я основывался на нём.
Время движения первого велосипедиста: t₁ = 24 ч.
Скорость первого велосипедиста: V₁ = 10 м/с = 36 км/ч.
Время движения второго велосипедиста: t₂ = 36 ч.
Путь первого велосипедиста: S₁ = V₁t₁.
Путь первого велосипедиста: S₂ = V₂t₂.
Они проехали одинаковый путь, т. е. S₁ = S₂.
Тогда: V₁t₁ = V₂t₂.
Выразим скорость второго велосипедиста:
(км/ч).
Так как объемы тел одинаковые, то, поскольку равновесие весов не нарушилось, одинаковыми будут и моменты сил, действующих на эти тела при погружении в жидкости. Тогда:
Найдем d₁/d₂:
Так как до погружения в жидкость весы находились в равновесии, то:
M₁ = M₂ => m₁gd₁ = m₂gd₂ => d₁/d₂= ρ₀₂gV : ρ₀₁gV = ρ₀₂/ρ₀₁ =
= 6150 : 9800 ≈ 0,63
Так как плотность первой жидкости 790 кг/м³, то плотность второй:
ρ₂ = ρ₁ * d₁/d₂ = 790*0,63 = 496 (кг/м³)
ответ: 496 кг/м³
Смотрите мой "перевод" вашей задачи в комментариях к вопросу. Я основывался на нём.
По условию:Время движения первого велосипедиста: t₁ = 24 ч.
Скорость первого велосипедиста: V₁ = 10 м/с = 36 км/ч.
Время движения второго велосипедиста: t₂ = 36 ч.
Скорость второго велосипедиста: V₂ - ?Решение:Путь первого велосипедиста: S₁ = V₁t₁.
Путь первого велосипедиста: S₂ = V₂t₂.
Они проехали одинаковый путь, т. е. S₁ = S₂.
Тогда: V₁t₁ = V₂t₂.
Выразим скорость второго велосипедиста: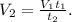
Численно получим: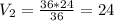
(км/ч).
ответ: 24 км/ч.