На малому поршні гідравлічнлї машини є вантаж масою 20 кг, а на великому - масою 200 кг. Площа малого поршня 400см квадратних. Яка площа великого поршня, якщо поршні перебувають в рівновазі?

Дано:m1(масла)=100 г=0,1 кг
         t1=20C=293 K
         cмасла(удельная теплоемкость вещества)=2,43*10³ Дж/кг*К
         m2(меди)=50 г=0,05 кг
          смеди=0,4*10³ Дж/кг*К
          t2=200C=473.15 K
Найти t3(масла)=?
Составляем уравнение теплового баланса, где медь отдает свое тепло, а масло принимает
Количество теплоты, необходимое для  нагревания масла: Qмасла=cмасла*m*(t3-t1)
Количество теплоты, отдающая медью  : Q меди=cмеди*m(t2-t1)
т.к. вся теплота меди пойдет на нагревании масла Qмасла=Q меди
смасла*m1(t3-t1)=смеди*m(t2-t3)
2.43*10³*0.1*(t3-293)=0.4*10³*0.05*(473.15-t3)
0.263*10³t3=80.662*10³
t3=306.7 K=33.55 C
ответ: температура масла в калориметре установится на 33,55 С

-0,6 м/c

Объяснение:

Скорость - есть производная расстояния. График представляет собой прямую с уравнением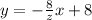 , где - абсцисса точки пересечения графика функции с осью Ot (z = const). Тогда 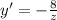(1), что и есть проекция скорости в любое время на ось Ox. По рисунку видно, что 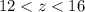(2). Отбросим положительные ответы, т.к. при подстановке в уравнение (1) они дают отрицательное z, что неверно по условию (2). Подставим в уравнение (1) 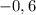, тогда из 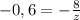получим 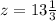, что подходит по условию (2). Убедимся, что ответ не 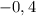: 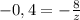, откуда 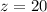, что не удовлетворяет условию (2).