Наблюдение поведения масла в воде Последовательность проведения опыта: Возьмите с пипетки несколько капель масла. Опустите пипетку на глубину 3 – 4 см в стакан с водой. Выпустите масло и пронаблюдайте, что происходит. Сформулируйте вывод.
Легко! Пусть t = 20000 секунд (я ввел эту величину для удобства). 1) Найдем количество целых часов в t. Для этого поделим t на количество секунд в одном часе (в часе 3600 секунд). Итак,. Отбрасываем дробную часть, она нам не нужна. Для дальнейшей работы нам понадобится остаток от предыдущего деления. Найдем его: . Итак, выходит, что в t ровно 5 целых часов и плюс еще 2000 секунд. 2) Теперь поработаем с этим остатком. Можно найти, сколько минут «вмещается» в 2000 секунд. Для этого поделим эти 2000 секунд на количество секунд в минуте (в минуте 60 секунд). Итак, . Снова отбрасываем дробную часть и снова находим остаток: . Итак, выходит, что в 2000 секунд «вмещается» 33 целых минуты и еще 20 секунд. --------- Так и запишем: t = 5 часов 33 минуты 20 секунд.
Решение. В системе отсчета "земля" начало координат свяжем с городом, откуда отправились оба тела, а начало отсчета времени — с началом движения велосипедиста.
Согласно условию автомобиль двигался на время меньше, чем велосипедист. Таким образом, уравнение их движения будут иметь вид:
В тот момент, когда автомобилист догонит велосипедиста, они будут находиться в одной точке ().
Имеем систему уравнений, левые части которых равны, а следовательно, и правые части равны, т. е.
Отсюда выразим время :
Определим значение искомой величины:
ч
Определим расстояние встречи автомобилиста и велосипедиста (момент, когда автомобилист начнет перегонять велосипедиста).
аналитический).
Расстояние, на котором автомобилист догонит велосипедиста, равняется их общей координате. Найдем ее как координату велосипедиста:
км
графический).
Запишем уравнения движения () велосипедиста и автомобиля:
Построим их графики (смотрите вложение). Точка пересечения графиков будет определять координату места, где автомобиль догонит велосипедиста, и время, когда это произойдет.
ответ: автомобиль догонит велосипедиста через 4 ч после выезда велосипедиста на расстоянии 80 км от города.
1) Найдем количество целых часов в t. Для этого поделим t на количество секунд в одном часе (в часе 3600 секунд). Итак,
2) Теперь поработаем с этим остатком. Можно найти, сколько минут «вмещается» в 2000 секунд. Для этого поделим эти 2000 секунд на количество секунд в минуте (в минуте 60 секунд). Итак,
---------
Так и запишем:
t = 5 часов 33 минуты 20 секунд.
Дано:
Найти: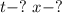
Решение. В системе отсчета "земля" начало координат свяжем с городом, откуда отправились оба тела, а начало отсчета времени — с началом движения велосипедиста.
Согласно условию автомобиль двигался на время меньше, чем велосипедист. Таким образом, уравнение их движения будут иметь вид:
меньше, чем велосипедист. Таким образом, уравнение их движения будут иметь вид:
В тот момент, когда автомобилист догонит велосипедиста, они будут находиться в одной точке (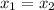 ).
).
Имеем систему уравнений, левые части которых равны, а следовательно, и правые части равны, т. е.
Отсюда выразим время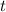 :
:
Определим значение искомой величины:
Определим расстояние встречи автомобилиста и велосипедиста (момент, когда автомобилист начнет перегонять велосипедиста).
встречи автомобилиста и велосипедиста (момент, когда автомобилист начнет перегонять велосипедиста).
аналитический).
Расстояние, на котором автомобилист догонит велосипедиста, равняется их общей координате. Найдем ее как координату велосипедиста:
графический).
Запишем уравнения движения (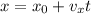 ) велосипедиста и автомобиля:
) велосипедиста и автомобиля:
Построим их графики (смотрите вложение). Точка пересечения графиков будет определять координату места, где автомобиль догонит велосипедиста, и время, когда это произойдет.
ответ: автомобиль догонит велосипедиста через 4 ч после выезда велосипедиста на расстоянии 80 км от города.