Определи дефект масс изотопа фтора F928.

Масса ядра изотопа фтора равна m = 28,03567 а. е. м.

Масса свободного протона равна mp = 1,00728 а. е. м.

Масса свободного нейтрона равна mn = 1,00866 а. е. м.
(ответ запиши с точностью до стотысячных, т. е. пять цифр после запятой).

ответ: Δm =
а. е. м.

Дано:

R = 0,5 м

m = 10 кг

t = 5 с

F = 50 Н

L - ?

Основное уравнение динамики вращательного движения:

I*ε = M

I = mR²/2 - момент инерции диска

M = F*R - момент силы

ε = M/I = Δω/Δt - угловое ускорение

На диск через верёвку действует сила F, которая приводит его во вращение. Момент импульса диска L равен:

L = I*ω

ε = Δω/Δt = (ω - ω₀)/(t - t₀), где ω₀, t₀ = 0 => ε = ω/t => ω = ε*t

L = I*ω = I*ε*t = I*(M/I)*t = M*t = F*R*t = 50*0,5*5 = 125 кг*м²/с

Решить можно и через теорему об изменении кинетической энергии:

∑A = ΔEк - сумма всех внешних сил, действующих на тело, равна изменению его кинетической энергии

∑A = A(F) = F*s

s = φ*R

φ = ε*t²/2 - диск приходит во вращение из состояния покоя =>

=> A(F) = F*(ε*t²/2)*R = F*(ω*t/2)*R = F*R*ω*t/2

ΔЕк = Ек - Eк₀ = Iω²/2 - Iω₀²/2; Iω₀²/2 = 0 => ΔЕк = Iω²/2

F*R*ω*t/2 = Iω²/2 | * (2/ω)

F*R*t = I*ω = L = 125 кг*м²/с

ответ: 125 кг*м²/с.

метра, или 30 см.

Объяснение:

Манометрическое давление в трубопроводе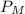 равно 37278 Н/м2.

Манометрическое давление, это давление, превышающее атмосферное, то есть разность между давлением в рассматриваемой точке пространства и атмосферным давлением: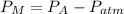 (1).

Центр трубопровода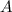 расположен на высоте 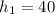см выше линии разделения между водой и ртутью, то есть выше точки 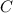и точки 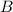соответственно.

Для начала найдем давление в точке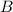 . Данная точка расположена ниже точки 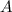на 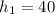см, следовательно давление в точке :

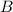Точку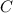 примем на одинаковой высоте с точкой 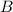, поэтому в этой точке давление будет такое же, как и в точке :

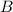Где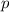 - плотность воды, равная 1000 кг/м3.

Давление в точке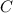 будет являться границей между водой и ртутью, поэтому если рассматривать давление со стороны ртути, то получим:

Где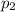 - плотность ртути, равна 13600 кг/м3.

Приравнивая эти выражения, получим:

Откуда будет равна:

Используя условия (1), получим:

метра, или 30 см.