Равнодействующая - это геометрическая сумма всех отдельно действующих сил:
R = F1 + F2 + F3
Согласно условию задачи, силы могут иметь два направления: вверх или вниз. Если направить оси Y традиционно вверх, то сила, сонаправленная с осью, будет иметь знак "+", а противонаправленная - "-". В условиях задачи предлагается всего четыре варианта равнодействующей. Всем четырём удовлетворяет только один ответ: 1 Н, 3 Н и 7 Н. Проверим:
1 + 3 + 7 = 11
7 + (-3) + (-1) = 7 - 3 - 1 = 3
7 + (-1) + 3 = 7 - 1 + 3 = 9
7 + (-3) + 1 = 5
Вообще здесь работают свойства сложения чётных и нечётных чисел. Смысл такой: поскольку равнодействующая сил имеет нечётное значение (3, 5, 9 или 11), то числа, из которых складывается это нечётное значение, должны быть чётным и нечётным (одно чётное + одно нечётное = нечётное). Так как у нас три силы, а не две, то одна из сил должна иметь нечётное значение, а сумма двух других - чётное.
--------------------------------------------------------------------------------------------------------------
Задание 1
Дано:
c = 130 Дж/кг⋅°С
mсв (масса свинца) = 77 г = 0.077 кг
mб (масс абензина+ = 12 г = 0.012 кг
tн = 24 °С
tк = 327 °С
λ = 0,25·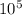
Дж/кг
q = 47⋅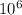
Дж/кг.
Найти:
ΔQ - ?
ΔQ = Qз - Qп
Qз = qmб (кол-во тепла, которое выделилось при сгорании бензина)
Qп = Q1 + Q2
Q1 = cmсвΔt (Δt - это разница температур, то бишь (tк - tн)) (кол-во энергии, которое уйдет на нагрев свинца до температуры плавления)
Q2 = λmсв (кол-во энергии, которое уйдет на плавление свинца)
ΔQ = qmб - (cmсвΔt + λmсв)
ΔQ = qmб - mсв(cΔt + λ)
Подставляем значения:
ΔQ = 47⋅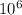
* 0.012 - 0.077*(130*(327 - 24) + 0,25·
)
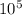Считаем:
ΔQ = 564000 - 4958.03
ΔQ = 559041.97 Дж
ΔQ = 559 кДж
ΔQ = 559 кДж
--------------------------------------------------------------------------------------------------------------
Задание 2
Дано:
c(с) = 201 Дж/°С
c(в) = 4200 Дж/°С,
L = 2260000 Дж/кг
λ =330000 Дж/кг
Vв = 2 л
mл = 1.2 кг
tн = 0°С
tк = 14°С
tп = 100°С
Найти:
mп - ?
Q1+Q2+Q3=Q4+Q5;
Q1 = λmл
Q2 = c(с)Δt (Δt - это разница температур, то бишь (tк - tн)
Q3 = cmобщΔt (mобщ - сумма масс воды и растопленного льда)
Q4 = Lmп
Q5 = cmпΔt (Δt - это разница температур 100 и 14 градусов) (tп - tк)
Подставляем:
λmл + c(с)(tк - tн) + cmобщ(tк - tн) = Lmп + cmпc(tп - tк)
λmл + c(с)(tк - tн) + cmобщ(tк - tн) = мп(L + c(tп - tк))
mобщ найдем, как сумму масс воды и льда
мобщ = мв + мл
mв=Pv
мобщ =Pv + mл
мобщ= 1000*0.002 + 1.2
мобщ = 3.2 кг
Выражаем мп:
мп = λmл + c(с)(tк - tн) + cmобщ(tк - tн) / L + c(tп - tк)
Подставляем значения:
мп = 330000*1,2 кг + 201*(14-0) + 4200*3.2*(14-0) / 2260000 + 4200*(100-14)
Высчитываем:
мп = 586974 / 2621200 = 0.224 кг = 224г
мп = 224г
--------------------------------------------------------------------------------------------------------------
Задание 3
ответ: точка росы равна 1°С, поэтому роса не выпадет
--------------------------------------------------------------------------------------------------------------Задание 4
ответ: водяной пар станет насыщенным при температуре 18°С
--------------------------------------------------------------------------------------------------------------
ИнтернетУрок, да? Не стыдно?
Равнодействующая - это геометрическая сумма всех отдельно действующих сил:
R = F1 + F2 + F3
Согласно условию задачи, силы могут иметь два направления: вверх или вниз. Если направить оси Y традиционно вверх, то сила, сонаправленная с осью, будет иметь знак "+", а противонаправленная - "-". В условиях задачи предлагается всего четыре варианта равнодействующей. Всем четырём удовлетворяет только один ответ: 1 Н, 3 Н и 7 Н. Проверим:
1 + 3 + 7 = 11
7 + (-3) + (-1) = 7 - 3 - 1 = 3
7 + (-1) + 3 = 7 - 1 + 3 = 9
7 + (-3) + 1 = 5
Вообще здесь работают свойства сложения чётных и нечётных чисел. Смысл такой: поскольку равнодействующая сил имеет нечётное значение (3, 5, 9 или 11), то числа, из которых складывается это нечётное значение, должны быть чётным и нечётным (одно чётное + одно нечётное = нечётное). Так как у нас три силы, а не две, то одна из сил должна иметь нечётное значение, а сумма двух других - чётное.
(1 + 3) = 4 (чётное) + 7 (нечётное) = 11 (нечётное)
(7 + (-3)) = 4 (чётное) + (-1) (нечётное) = 3 (нечётное)
(7 + (-1)) = 6 (чётное) + 3 (нечётное) = 9 (нечётное)
(7 + (-3)) = 4 (чётное) + 1 (нечётное) = 5 (нечётное)
Остальные варианты ответа не подходят, поскольку не во всех суммах получаются заданные значения равнодействующей. Например:
8 + 0,5 + 2,5 = 11 - подходит
8 + (-0,5) + (-2,5) = 5 - подходит
8 + (-0,5) + 2,5 = (8 + (-0,5)) + 2,5 = 10 - не подходит
или 8 + (-2,5) + 0,5 = (8 + (-2,5)) + 0,5 = 6 - не подходит
Последние две суммы, которые не подходят, иллюстрируют свойство сложения двух нечётных чисел - в таком случае всегда получается чётное число.
ответ: 1 Н, 3 Н и 7 Н.