Количество ядер радиоактивного вещества, оставшееся через определенное время, можно рассчитать по уравнению N = N0 * (1/2)^(t/T), где N0 - начальное количество ядер время, а T - период полураспада вещества.
В данном случае начальное число ядер N0 равно 1000000, период полураспада T составляет 164 дня, и мы хотим найти число ядер через один день (t = 1 день). Подставляя эти значения, мы получаем:
N = 1000000 * (1/2)^(1/164) = 999308
Таким образом, через один день от первоначальных 1000000 осталось примерно 999308 ядер кальция.
Чтобы стержень не вращался вокруг некоторой точки, полный момент всех внешних сил относительно этой точки должен быть равен нулю. Из этого условия и определим, через какую точку необходимо провести ось вращения. Поскольку у нас всего две силы, можно сразу заключить, что искомая точка находится справа от точки 3. Иначе обе силы вращали бы рычаг против часовой стрелки, и не уравновешивали бы друг друга.
Обозначим расстояние между любыми двумя соседними точками через ''L'', а расстояние от точки 3 до искомой точки через ''x''. Тогда сила F2 вращает стержень по часовой стрелке и и ее момент равен *x. Сила F1 вращает стержень против часовой стрелки, и ее момент равен *(x + 2L).
Приравняем эти два момента и решим линейное уравнение найдя ''x'':
, т.е. вправо на одно деление, а это точка 4.
Следовательно, ось вращения нужно расположить в точке 4
Количество ядер радиоактивного вещества, оставшееся через определенное время, можно рассчитать по уравнению N = N0 * (1/2)^(t/T), где N0 - начальное количество ядер время, а T - период полураспада вещества.
В данном случае начальное число ядер N0 равно 1000000, период полураспада T составляет 164 дня, и мы хотим найти число ядер через один день (t = 1 день). Подставляя эти значения, мы получаем:
N = 1000000 * (1/2)^(1/164) = 999308
Таким образом, через один день от первоначальных 1000000 осталось примерно 999308 ядер кальция.
C) точка 4
Объяснение:
Чтобы стержень не вращался вокруг некоторой точки, полный момент всех внешних сил относительно этой точки должен быть равен нулю. Из этого условия и определим, через какую точку необходимо провести ось вращения. Поскольку у нас всего две силы, можно сразу заключить, что искомая точка находится справа от точки 3. Иначе обе силы вращали бы рычаг против часовой стрелки, и не уравновешивали бы друг друга.
Обозначим расстояние между любыми двумя соседними точками через ''L'', а расстояние от точки 3 до искомой точки через ''x''. Тогда сила F2 вращает стержень по часовой стрелке и и ее момент равен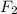
*x. Сила F1 вращает стержень против часовой стрелки, и ее момент равен 
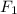*(x + 2L).
Приравняем эти два момента и решим линейное уравнение найдя ''x'':
Следовательно, ось вращения нужно расположить в точке 4