Поднимая с подвижного и неподвижного блоков ящик массой 16 кг на высоту 5 м, вытянули часть каната длиной 10 м. При этом действовали силой 100 Н. Каков КПД этой системы блоков? Укажите правильный вариант ответа:
Разделим молекулы на две группы: те, что абсолютно упруго соударяются со стенкой, и те, что к стенке прилипают.
Давление в первой группе , а во второй - ; Тогда ;
Заметим, что давление пропорционально средней силе, которая оказывается молекулами на стенку сосуда, которая в свою очередь (согласно второму закону Ньютона), пропорциональна изменению импульса падающих молекул. Для первой группы изменение импульса (суммарное) равно , а для второй - ; Тогда , где - постоянная для рассматриваемого газа. Аналогично ; Изначально , т.е. ;
Разделим молекулы на две группы: те, что абсолютно упруго соударяются со стенкой, и те, что к стенке прилипают.
Давление в первой группе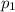
, а во второй - 
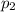; Тогда 
;
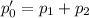Заметим, что давление пропорционально средней силе, которая оказывается молекулами на стенку сосуда, которая в свою очередь (согласно второму закону Ньютона), пропорциональна изменению импульса падающих молекул. Для первой группы изменение импульса (суммарное) равно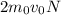
, а для второй - 
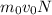; Тогда 
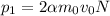, где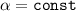 
- постоянная для рассматриваемого газа. Аналогично 
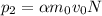; Изначально 
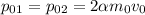, т.е. 
;
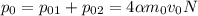А теперь: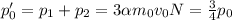
ответ: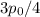
Давление жидкости на дно сосуда:
p = ρgh, где ρ - плотность жидкости, кг/м³
g = 9,8 H/кг - ускорение своб. падения
h - высота столба жидкости, м
1). От плотности. Чем больше плотность жидкости, тем большее давление она оказывает при одной и той же высоте столба.
2). От ускорения свободного падения. При удалении от поверхности Земли ускорение свободного падения уменьшается:
где G = 6,67·10⁻¹¹ H·м²/кг² - гравитационная постоянная
М = 6·10²⁴ кг - масса Земли
R = 6,38·10⁶ м - радиус Земли
h - высота над поверхностью Земли
3). От высоты столба жидкости. Чем больше высота, тем большее давление одна и та же жидкость оказывает на дно сосуда.