1) Для начала мы сделаем рисунок про массивное тело подвешено на невесомой и нерастяжимой нити, чтобы было понятно. (Рисунок сделан внизу).
2) Для начала мы воспользуемся законом сохранения энергий, про этого закона мы найдем максимальную скорость тела:
E(понт.) = E(кин.) - закон сохранения энергий
E(понт.) = mgh - потенциальная энергия
E(кин.) = (m×(υ(max.))²)/2 - кинетическая энергия
Следовательно мы получаем:
mgh = (m×(υ(max.))²)/2 | : m
gh = (υ(max.))²/2 | × 2
2gh = (υ(max.))² ⇒ υ(max.) = √(2gh) - максимальная скорость тела (1)
3) Теперь мы еще в условий сказано что нить с телом отклонили на 60° от вертикали и отпустили - это значит что получится прямоугольный треугольник, потому что нить с телом отклонили на 60° от вертикали и отпустили его вниз. По рисунку мы видим что получился прямоугольный треугольник, но нам надо найти высоту которую тело отпустили, следовательно мы получим:
Пусть гипотенуза нерастяжимой нити - , тогда маленький катет - .
Теперь мы находим высоту, которую указан на рисунке:
- высота которую тело опустили (2)
3) Теперь мы находим общую формулу про максимальную скорость тела пользуясь из (1) и (2), тогда мы получим:
υ(max.) = √(2gh) и h = l/2, следовательно:
υ(max.) = √(2g × (l/2)) = √(g×l) ⇒ υ(max.) = √(g×l) - максимальная скорость тела
Достигнув высоты 1100 метров, тело имело какую-то скорость V0. тогда за 10 с тело путь: S-S1, где S=1100, S2=120 но за эти же 10 тело расстояние равное : S-S1=Vot+g*t^2/2 Vo=(2(S-S1)-g*t^2)/2*t - мы нашли скорость, которую развило тело, когда оно начало падать с высоты 1100м Т.к тело начало падать свободно, то эту же скорость оно развило за время t0=Vo/g. Тогда расстояние, которое тело до 1100 м можно вычислить S2=g*t0^2/2=((2(S-S1)-g*t^2)^2)/8gt^2 а общая высота : S+S2=((2(S-S1)-g*t^2)^2)/8gt^2+S=(2*980-980)^2/8*9.8*100+1100=122,5+1100=1222,5м
Дано:
l = 90 см = 0,9 м
α = 60°
------------------------------
Найти:
υ(max.) - ?
1) Для начала мы сделаем рисунок про массивное тело подвешено на невесомой и нерастяжимой нити, чтобы было понятно. (Рисунок сделан внизу).
2) Для начала мы воспользуемся законом сохранения энергий, про этого закона мы найдем максимальную скорость тела:
E(понт.) = E(кин.) - закон сохранения энергий
E(понт.) = mgh - потенциальная энергия
E(кин.) = (m×(υ(max.))²)/2 - кинетическая энергия
Следовательно мы получаем:
mgh = (m×(υ(max.))²)/2 | : m
gh = (υ(max.))²/2 | × 2
2gh = (υ(max.))² ⇒ υ(max.) = √(2gh) - максимальная скорость тела (1)
3) Теперь мы еще в условий сказано что нить с телом отклонили на 60° от вертикали и отпустили - это значит что получится прямоугольный треугольник, потому что нить с телом отклонили на 60° от вертикали и отпустили его вниз. По рисунку мы видим что получился прямоугольный треугольник, но нам надо найти высоту которую тело отпустили, следовательно мы получим:
Пусть гипотенуза нерастяжимой нити -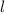
, тогда маленький катет - 
.
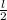Теперь мы находим высоту, которую указан на рисунке:
3) Теперь мы находим общую формулу про максимальную скорость тела пользуясь из (1) и (2), тогда мы получим:
υ(max.) = √(2gh) и h = l/2, следовательно:
υ(max.) = √(2g × (l/2)) = √(g×l) ⇒ υ(max.) = √(g×l) - максимальная скорость тела
υ(max.) = √(9,8 м/с² × 0,9 м) = √(8,82 м²/с²) ≈ 2,97 м/с
ответ: υ(max.) = 2,97 м/с
тогда за 10 с тело путь: S-S1, где S=1100, S2=120
но за эти же 10 тело расстояние равное :
S-S1=Vot+g*t^2/2
Vo=(2(S-S1)-g*t^2)/2*t - мы нашли скорость, которую развило тело, когда оно начало падать с высоты 1100м
Т.к тело начало падать свободно, то эту же скорость оно развило за время t0=Vo/g.
Тогда расстояние, которое тело до 1100 м можно вычислить
S2=g*t0^2/2=((2(S-S1)-g*t^2)^2)/8gt^2
а общая высота :
S+S2=((2(S-S1)-g*t^2)^2)/8gt^2+S=(2*980-980)^2/8*9.8*100+1100=122,5+1100=1222,5м