Так как скорость мальчика составляет долю 0,6 от скорости течения реки, то перемещение мальчика не может быть направлено перпендикулярно течению реки. В этом можно убедится, сделав следующие построения. Обозначим скорость течения u (на рисунке направлена горизонтально, 5 клеточек), скорость мальчика относительно реки обозначи v₀ (v₀=nu, по условию задачи n=0,6; однако стоит отметить, что в конце задачи получим формулу для решения любого n, при условии, что 0<n≤1) (v₀ возьмем за 3 клеточки). Чтобы найти вектор направления скорости мальчика относительно берега V, нам надо знать точку конца этого вектора. Для этого из конца вектора u проведем окружность радиуса v₀. Обращаем внимание, что если провести касательную АВ (см. рис.), то, т.к. вектор перемещения сонаправлен с вектором скорости V, то расстояние, на которое снесет мальчика ΔX=BC окажется наименьшим при данной скорости относительно реки v₀ (это и есть оптимальная стратегия!). Итак, мы получили прямоугольный треугольник АВС, в котором ΔX=BC (смещение, которое нужно найти), L=AC (ширина реки, по условию 120 м) и AB (перемещение мальчика относительно берега),
1. Введем прямоугольную систему координат. Ось Оу направлена перпендикулярно течению, Ох - вдоль реки.
2. Мальчик участвует в двух движениях одновременно: он перемещается вдоль берега (Ох) со скоростью V*cosα = u - v₀*cosα, и он плывет перпендикулярно течению (Оу) со скоростью v₀*sinα.
Пусть время t - время за которое мальчик переплывет реку. Так как он плывет равномерно прямолинейно, то согласно законам кинематики:
ΔX=(u-v₀*cosα)t (1)
L=v₀*sinα*t (2)
3. Так как направление скорости V совпадает с касательной, то по св-ву касательной вектор V перпендикулярен вектору v₀. Таким образом u*cosα=v₀.
С другой стороны v₀=nu, значит cosα=n, согласно осн. тригонометрическому тождеству: sinα=√1-
4. Из равенств 1 и 2 следует, что:
((u-v₀*cosα)*L) / (v₀*sinα)=ΔX
И в итоге:
ΔX = (L/n) * √
В нашем случае:
ΔX = 160 м
Напоминаю, что полученная формула справедлива для любого 0<n≤1
1) Ek0 = Ek + Ep, Ek = Ep, Ek0 = 2Ep, mv0^2 / 2 = 2mgh, h = v0^2 / (4g),
h = 49^2 / 4*9.8 = 61,25 м
2) mv0^2 / 2 = mgh + mv^2 / 2, v = корень(v0^2 - 2gh) = корень(15^2 - 2*10*10) = 5м/с
3) mv0^2 / 2 = mgh + mv^2 / 2, v = v0/2, mv0^2 / 2 = mgh + mv0^2 / 8, 3mv0^2 / 8 = mgh, h = 3v0^2 / 8g, h = 3*10^2 / 8*10 = 3.75 м
4) A = Ek - Ek0 = mv^2 / 2 - mv0^2 / 2 = m/2(v^2 - v0^2), A = 0.5 кг/2(16^2 - 20^2) = -36 Дж
5) mv^2 / 2 - mgh = -FS, F = m/s(gh - v^2 / 2), F = 60/500(10*10 - 8^2 / 2) = 8.16 H
6) Ek0 = Ek + Ep, Ek = Ep, Ek0 = 2Ep, mv0^2 / 2 = 2mgh, h = v0^2 / (4g), h = 16^2 / 4*9.8 = 6,5 м
(качественный анализ)
Так как скорость мальчика составляет долю 0,6 от скорости течения реки, то перемещение мальчика не может быть направлено перпендикулярно течению реки. В этом можно убедится, сделав следующие построения. Обозначим скорость течения u (на рисунке направлена горизонтально, 5 клеточек), скорость мальчика относительно реки обозначи v₀ (v₀=nu, по условию задачи n=0,6; однако стоит отметить, что в конце задачи получим формулу для решения любого n, при условии, что 0<n≤1) (v₀ возьмем за 3 клеточки). Чтобы найти вектор направления скорости мальчика относительно берега V, нам надо знать точку конца этого вектора. Для этого из конца вектора u проведем окружность радиуса v₀. Обращаем внимание, что если провести касательную АВ (см. рис.), то, т.к. вектор перемещения сонаправлен с вектором скорости V, то расстояние, на которое снесет мальчика ΔX=BC окажется наименьшим при данной скорости относительно реки v₀ (это и есть оптимальная стратегия!). Итак, мы получили прямоугольный треугольник АВС, в котором ΔX=BC (смещение, которое нужно найти), L=AC (ширина реки, по условию 120 м) и AB (перемещение мальчика относительно берега),
1. Введем прямоугольную систему координат. Ось Оу направлена перпендикулярно течению, Ох - вдоль реки.
2. Мальчик участвует в двух движениях одновременно: он перемещается вдоль берега (Ох) со скоростью V*cosα = u - v₀*cosα, и он плывет перпендикулярно течению (Оу) со скоростью v₀*sinα.
Пусть время t - время за которое мальчик переплывет реку. Так как он плывет равномерно прямолинейно, то согласно законам кинематики:
ΔX=(u-v₀*cosα)t (1)
L=v₀*sinα*t (2)
3. Так как направление скорости V совпадает с касательной, то по св-ву касательной вектор V перпендикулярен вектору v₀. Таким образом u*cosα=v₀.
С другой стороны v₀=nu, значит cosα=n, согласно осн. тригонометрическому тождеству: sinα=√1-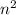
4. Из равенств 1 и 2 следует, что:
((u-v₀*cosα)*L) / (v₀*sinα)=ΔX
И в итоге:
ΔX = (L/n) * √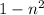
В нашем случае:
ΔX = 160 м
Напоминаю, что полученная формула справедлива для любого 0<n≤1
ответ: 160 м