Для выполнения данной задачи нам необходимо знать свою массу, а также высоту этажа школы. Например, наша масса составляет 70 кг, а высота этажа равна 3,5 м. Теперь засечем, за какое время мы поднимаемся с первого на второй этаж, пусть это время равно 17 секунд. Тогда воспользуемся формулой мощности:
Это решение задачи для случая, когда мы поднимаемся по лестнице не спеша. Теперь посчитаем, какую мощность мы развиваем, если будем подниматься по лестнице быстро. Предположим, что время подъема по лестнице будет равно 7 секунд. Подставим это время в формулу мощности:
Данные пробирки имеют одинаковую частоту вращения, но разные линейные скорости, так как одна пробирка находится дальше другой от центра центрифуги. Пусть r₁ = R – радиус окружности, описываемый первой пробиркой, тогда r₂ = (R - 11) – это радиус окружности, по какой движется вторая пробиркой. Циклические частоты пробирок одинаковы ⇒ ω₁ = ω₂, а линейные скорости по условию равны: v₁ = 56 м/с, v₂ = 34 м/с
По формуле из кинематики: v₁ = ω₁·r₁, v₂ = ω₂·r₂ ⇒ ω₁ = v₁/r₁ = ω₂ = v₂/r₂ ⇒ v₁/R = v₂/(R - 11) ⇒ (по правилу пропорции) v₁ · (R - 11) = v₂ · R ⇒
R · (v₁ - v₂) = 11 · v₁ ⇒ R = сантиметров
ответ: первая пробирка описывает окружность радиусом в 28 см.
Для выполнения данной задачи нам необходимо знать свою массу, а также высоту этажа школы. Например, наша масса составляет 70 кг, а высота этажа равна 3,5 м. Теперь засечем, за какое время мы поднимаемся с первого на второй этаж, пусть это время равно 17 секунд. Тогда воспользуемся формулой мощности:
N = A/t = FS/t = mgS/t = 70 • 9,8 • 3,5/17 = 141,24 Вт
Это решение задачи для случая, когда мы поднимаемся по лестнице не спеша. Теперь посчитаем, какую мощность мы развиваем, если будем подниматься по лестнице быстро. Предположим, что время подъема по лестнице будет равно 7 секунд. Подставим это время в формулу мощности:
N - A/t = FS/t = mgS/t = 70 • 9,8 • 3,5/7 = 343 Вт
Объяснение:Всее
Данные пробирки имеют одинаковую частоту вращения, но разные линейные скорости, так как одна пробирка находится дальше другой от центра центрифуги. Пусть r₁ = R – радиус окружности, описываемый первой пробиркой, тогда r₂ = (R - 11) – это радиус окружности, по какой движется вторая пробиркой. Циклические частоты пробирок одинаковы ⇒ ω₁ = ω₂, а линейные скорости по условию равны: v₁ = 56 м/с, v₂ = 34 м/с
По формуле из кинематики: v₁ = ω₁·r₁, v₂ = ω₂·r₂ ⇒ ω₁ = v₁/r₁ = ω₂ = v₂/r₂ ⇒ v₁/R = v₂/(R - 11) ⇒ (по правилу пропорции) v₁ · (R - 11) = v₂ · R ⇒
R · (v₁ - v₂) = 11 · v₁ ⇒ R =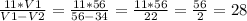
сантиметров
ответ: первая пробирка описывает окружность радиусом в 28 см.