Физика: в решении этой задачи с физики 8 класс

в решении этой задачи с физики 8 класс

Показать ответ

Ответ:

Konopleva1947lina

25.06.2021 00:05

11,25 м

Объяснение:

Если решать эту задачу по школьному, без привлечения инструментария матанализа, то рассуждать можно следующим образом, - в любой точке траектории ускорение свободного падения может быть разложено на две составляющих - вдоль касательной к траектории (нормальное ускорение) и вдоль нормали к траектории (центростремительное ускорение), нам нужна вторая величина, так как она позволяет рассчитать искомый радиус. В наивысшей точке подъема мяча, очевидно, что центростремительное ускорение целиком совпадает с ускорением свободного падения:

$\displaystyle \frac{v_x^2}{R}=g$

Откуда:

$\displaystyle R=\frac{v_x^2}{g}$

Горизонтальная составляющая скорости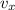 $\displaystyle v_x$ будет везде одинакова и равна (учтем что 54 км/ч=15 м/с):

$\displaystyle v_x=v_0cos\alpha =15*cos45^0=\frac{15}{\sqrt{2} }$ м/с

Искомый радиус кривизны траектории:

$\displaystyle R=\left(\frac{15}{\sqrt{2} }\right)^2 *\frac{1}{10}=11.25$ м.

0,0(0 оценок)

Ответ:

matvienko14

28.11.2021 07:55

До вылета снаряда импульс судна P1=(m1+m2)*v1= 200 050*54/3,6
=3000750 кг*м/с. После выстрела геометрическая сумма импульса судна и импульса снаряда равна импульсу судна до выстрела.Импульс снаряда P2=m2*v2=50 000 кг*м/с. После выстрела импульс судна стол равен P1*P1+P2*P2-2*P1*P2*cos(120)=3026059,82 кг*м/с, откуда скорость судна после выстрела =15,13 м/с. Но вектор скорости направлен к горизонтали под углом, косинус которого равен 0,999, так что "горизонтальная" скорость судна равна 15,13*0,999=15,128 м/с. Приращение скорости составило 0,128 м/с

0,0(0 оценок)

Популярные вопросы: Физика