Виписати значення амплітуди, циклічної частоти, та початкової фази наступних функцій: y=15sin(2x-56)

Показать ответ

Ответ:

максимус67

28.03.2023 17:50

1502 м

Объяснение:

Поскольку сопротивлением воздуха можно пренебречь, на тело действует только сила тяжести.

Рассмотрим вертикальный и горизонтальный полет отдельно.

Вертикальное движение мяча является равноускоренным с ускорением g.

Горизонтальное движение является равномерным.

Начальная вертикальная скорость:

${\displaystyle v_0_y=v_0*sin(45^\circ) = 50*\frac{\sqrt{2} }{2} =25\sqrt{2}\ m/s$

Начальная горизонтальная скорость:

${\displaystyle v_0_x=v_0*cos(45^\circ) = 50*\frac{\sqrt{2} }{2} =25\sqrt{2}\ m/s$

Полет заканчивается, когда мяч падает на землю.

Найдем время полета:

$0 = 2 + 25\sqrt{2} *t+\frac{-1.667*t^2}{2$

${\displaystyle -0.811 * t^2+25\sqrt{2}*t + 2 =0$

Получаем обычное квадратное уравнение. Решая его, при условии что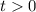 t 0 получаем

t = 42.474 s

За это время горизонтально мяч пролетит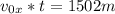 ${\displaystyle v_0_x * t = 1502 m$

Дмитрий бросает мяч со скоростью 50 м/c под углом 45 градусов к горизонту. На какое расстояние закин

0,0(0 оценок)

Ответ:

ДашинСамурай

18.09.2020 07:44

Дано:
$m_{1}=1$ кг
l=0,9

м
$\alpha =39$ °
$m_{2}=0,01$ кг
$v_{2}=300$ м/с
$v_{2}'=200$ м/с

Найти:
$\beta - ?$

Решение:

1) Изначально шар находится на некоторой высоте h1 с длиной нити l. Затем его опускают и в положении дальнейшего соударения с пулей шар имеет скорость V1. Запишем закон сохранения энергии:

$m_{1}g h_{1}= \frac{ m_{1} v_{1}в }{2}$

Сокращаем m1. Рассмотрим cosα:

$cos \alpha = \frac{l- h_{1} }{l}
$

Откуда выводим h1:

$h_{1}=l(1- cos \alpha )$

Выводим из ЗСЭ V1, подставляя формулу для h1:

$v_{1}= \sqrt{2gl(1-cos \alpha )}$

2) Закон сохранения импульса по горизонтали для пули и шара, спроецированный на некоторую ось ОХ, направленную в сторону движения пули, имеет вид:

$m_{2} v_{2}- m_{1} v_{1}= m_{2} v_{2}'- m_{1} v_{1}'$ ,

где V1' - скорость шара после соударения с пулей. Выведем ее:

$v_{1}'= \sqrt{2gl(1-cos \alpha )}- \frac{ m_{2}( v_{2}- v_{2}') }{ m_{1} } \\ \\ 
 v_{1}'= \sqrt{20*0,9*0,5}- \frac{0,01*100}{1}=3-1=2$

3) Закон сохранения энергии для шара после соударения с пулей:

$\frac{ m_{1} v_{1}'в }{2}= m_{1}g h_{2}$

При этом h2 аналогично h1 равен:

$h_{2} =l(1-cos \beta )$

Перепишем ЗСЭ в виде:

$v_{1}'в=2gl-2glcos \beta$

Откуда cosβ:

$cos \beta =1- \frac{ v_{1}'в }{2gl} =1- \frac{4}{18} = \frac{14}{18}= \frac{7}{9}=39$ °