Так как ничего не сказано, в какой точке системы координат находится ковбой изначально, и угол φ<360° говорит о произвольном направлении, то этот угол может быть каким угодно. Например, на рис.1 ковбой начал скакать из точки A под углом φ=90°, в точке М повернул налево под прямым углом и оказался в точке F с заданными координатами. А на рис.2 ковбой начал скакать из точки В под углом φ=45°, повернул налево под прямым углом в точке N и оказался в точке F, выполнив все условия задачи. Треугольники AMF и BNF можно вращать около точки F на любой угол, соответственно будет меняться угол φ. Вывод : если не заданы начальные координаты ковбоя, то угол φ может быть каким угодно.
Пусть ковбой начинает свой путь из точки начала координат О(0;0) - рис.3. Проскакав OP=6 км под углом φ к оси x, ковбой повернул налево под прямым углом в точке P и проскакал ещё PF=8 км.
Координаты точки F(-5; y>0).
ΔOPF : ∠P = 90°; OP = 6 км; PF = 8 км. Теорема Пифагора :
OF² = OP² + PF² = 6² + 8² = 100 = 10²
OF = 10 км - перемещение ковбоя
sin ∠FOP = PF/OF = 8/10 = 0,8 ⇒ ∠FOP = arcsin 0,8
ΔONF : ∠N = 90°; ON = 5 км; OF = 10 км - катет равен половине гипотенузы ⇒ ∠OFN = 30° ⇒ ∠NOF = 60°
Так как ничего не сказано, в какой точке системы координат находится ковбой изначально, и угол φ<360° говорит о произвольном направлении, то этот угол может быть каким угодно. Например, на рис.1 ковбой начал скакать из точки A под углом φ=90°, в точке М повернул налево под прямым углом и оказался в точке F с заданными координатами. А на рис.2 ковбой начал скакать из точки В под углом φ=45°, повернул налево под прямым углом в точке N и оказался в точке F, выполнив все условия задачи. Треугольники AMF и BNF можно вращать около точки F на любой угол, соответственно будет меняться угол φ. Вывод : если не заданы начальные координаты ковбоя, то угол φ может быть каким угодно.
==================================================
Пусть ковбой начинает свой путь из точки начала координат О(0;0) - рис.3. Проскакав OP=6 км под углом φ к оси x, ковбой повернул налево под прямым углом в точке P и проскакал ещё PF=8 км.
Координаты точки F(-5; y>0).
ΔOPF : ∠P = 90°; OP = 6 км; PF = 8 км. Теорема Пифагора :
OF² = OP² + PF² = 6² + 8² = 100 = 10²
OF = 10 км - перемещение ковбоя
sin ∠FOP = PF/OF = 8/10 = 0,8 ⇒ ∠FOP = arcsin 0,8
ΔONF : ∠N = 90°; ON = 5 км; OF = 10 км - катет равен половине гипотенузы ⇒ ∠OFN = 30° ⇒ ∠NOF = 60°
∠NOF + ∠FOP + φ = 180°
φ = 180° - ∠NOF - ∠FOP = 180° - 60° - arcsin 0,8 ≈
≈ 120° - 53,131° ≈ 66,869° ≈ 66,9°
ответ : φ ≈ 66,9°
12. Δx=8 см
16. Δx= 12 см
Объяснение:
12.
F=k*Δx
Δx=F/k=4/50=0.08 м = 8 см
16.
F=k*Δx
Δx=F/k=12/100=0.12 м = 12 см
15.
Второй закон Ньютона в векторной форме
Fрез(вектор)=ma(вектор)
F(вектор)+mg(вектор)=ma(вектор)
В проекции на ось совпадающей с направлением движения, то есть направленной вниз
F+mg=ma
F=-Fупр=k*дельтаХ
k*ΔХ+mg=ma
а=(k*ΔХ+mg)/m=29.8 м/с2
ΔХ=F/k=0,2 м
то есть мы м с ускорением 29,8 м/с2, определим максимальную скорость в конце пути
S=a*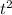
/2
t=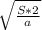
=0.116 с время когда мы набрали мак скорость
v=a*t=29.8*0.116=3.45 м/с