Який рух за формою траєкторії мають стрілки годинника, кину тий горизонально з певної висоти камінець, велосипедист на пово роті?

2. Укажіть позначення та одиницю періоду обертання в СІ. 3. Що називають частотою обертан

ня? 4. Яка різниця між обертальним та криволінійним рухами?

5. Як називають рух по колу, чис лове значення швидкості якого не змінюється?

6. Дайте характеристику оберталь ного руху.

7. Чим користувалися в давнину

для вимірювання часу? 8. Розрахуйте частоту обертання тіла, якщо період його обертан- ня

10 с.

9. Дайте означення повного оберту під час рівномірного обертально

го руху. 10. Наведіть формулу для розрахун ку періоду обертання.

11. Дайте означення періоду обер тання.

12. Які проміжки часу можна визна чити за зміною фаз Місяця?

Показать ответ

Ответ:

Kolla77

24.03.2020 02:20

Щенок Виталик едет по ленте транспортёра в гости к бабушке. Но было бы неинтересно путешествовать на обычном транспортере, поэтому транспортер не обычный, а двигающийся равноускоренно. От предвкушения близящейся встречи щенок от радости подпрыгивает вверх на одну секунду, затем едет по ленте в течении 1 секунды, затем ситуация повторяется. Через 4 секунды после начала путешествия лента сломалась - она не была предназначена для перевозки животных. На рисунке изображён график зависимости расстояния Виталика (в метрах) от времени (в секундах).

ВОПРОСЫ.
1) Как давно включилась лента транспортера? Считайте, что она стартовала с нулевой скоростью.
2) Больше или меньше проехал бы Виталик, если не подпрыгивал от волнения? На сколько?
3) Каково расстояние от места старта Виталика до его бабушки? Если бы транспортер не сломался, то Виталик, не меняя темпа подпрыгиваний, приехал бы к ней за 6 секунд.

РЕШЕНИЕ.
1. Скорость ленты сразу после запрыгивания Виталика равна угловому коэффициенту начального участка графика, т.е. 1 м/с.
2. Уравнение движения Виталика на втором участке S(t) = v0(t - 1) + a(t - 1)^2/2. Так как S(2 с) = 3 м, a = 2 м/с2.
3. v(t) = at -> Лента стартовала t = 1/1 = 1 с назад
4. Если бы Виталик не подпрыгивал, то двигался бы по закону S(t) = t + t^2, S(4) = 22 - на 12 метров больше
5. Пятую секунду Виталик движется равномерно со скоростью 5 м/с, проедет еще 5 м. Шестую секунду проедет 5 * 1 + 1^2 = 6 м.
Бабушка на расстоянии 10 + 5 + 6 = 21 м
Составьте свою , решение которой будет основано на умении «читать» графики. предложите свой вариант

Составьте свою , решение которой будет основано на умении «читать» графики. предложите свой вариант

0,0(0 оценок)

Ответ:

Elizabeth1006

20.05.2021 10:17

Дано:

$v_{1} = 20$ км/ч

$v_{2} = 80$ км/ч

$\tau = 3$ ч

Найти: $t - ? \ x - ?$

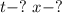
Решение. В системе отсчета "земля" начало координат свяжем с городом, откуда отправились оба тела, а начало отсчета времени — с началом движения велосипедиста.

Согласно условию автомобиль двигался на время $\tau$ меньше, чем велосипедист. Таким образом, уравнение их движения будут иметь вид:

$\left \{ {\bigg{x_{1} = v_{1}t \ \ \ \ \ \ \ \ } \atop \bigg{x_{2} = v_{2}(t - \tau)}} \right.$

В тот момент, когда автомобилист догонит велосипедиста, они будут находиться в одной точке (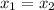 $x_{1} = x_{2}$ ).

Имеем систему уравнений, левые части которых равны, а следовательно, и правые части равны, т. е.

$v_{1}t = v_{2}(t - \tau)$

Отсюда выразим время :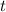

$t = \dfrac{v_{2}\tau}{v_{2} - x_{1}}$

Определим значение искомой величины:

$t = \dfrac{80 \cdot 3}{80 - 20} = 4$ ч

Определим расстояние встречи автомобилиста и велосипедиста (момент, когда автомобилист начнет перегонять велосипедиста).

аналитический).

Расстояние, на котором автомобилист догонит велосипедиста, равняется их общей координате. Найдем ее как координату велосипедиста:

$x = x_{1} = v_{1}t = 20 \cdot 4 = 80$ км

графический).

Запишем уравнения движения (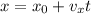 $x = x_{0} + v_{x}t$ ) велосипедиста и автомобиля:

$x_{1} = 20t\\x_{2} = 80(t-3)$

Построим их графики (смотрите вложение). Точка пересечения графиков будет определять координату места, где автомобиль догонит велосипедиста, и время, когда это произойдет.

ответ: автомобиль догонит велосипедиста через 4 ч после выезда велосипедиста на расстоянии 80 км от города.