Заряды 2 q и q (рис.№ 2) создают электрическое поле. Потенциал в точке В равен 90В. Расстояние АВ=ВС=СD= r
А=2q C=q
A. Запишите принцип суперпозиции полей для потенциалов [1]
B. Запишите формулы потенциалов точечных зарядов и применяя принцип
суперпозиции полей, выразите расстояние r [1]
C. Вычислите потенциал в точки D двух зарядов

Показать ответ

Ответ:

Cherry5858

20.05.2023 07:58

Жер шары бетінің жалпы ауданы 510,2 млн.км-ге тең. Ол материктер мен мұхиттарға бөлінген. Құрлықты құрайтын материктер мен аралдар үлесіне шамамен 149,1 млн км немесе бүкіл Жер бетінің29,2%-ы келеді.

Жер шарында барлығы алты материк бар. Материктер қалыптасуы мен қазіргі табиғат ерекшеліктеріне сәйкес, солтүстік және оңтүстік жарты шар материктеріне топтастырылып, мынадай тәртіппен қарастырылады: Еуразия (54 млн км астам), Солтүстік Америка (24,2 млн км), Оңтүстік Америка (18,3 млн км), Африка (30,3 млн км), Аустралия мен Мұхит аралдары (9,0 млн км-ге жуық), Антарктика (14 млн км). Материктерге таяу жағалаудағы қайраңдар мен материктік беткейлерде материктік аралдар орналасқан. Олар – жер қыртысындағы қозғалыстар әсерінен құрлықтың кейіннен бөлініп қалған бөліктері, көбінесе ауданы ауқымды келеді (Гренландия, Мадагаскар, Британ аралдары және т.б.). Мұхиттардың қозғалмалы бөліктерінде жанартаулық аралдар (Исландия, Гавай, Азор аралдары), ал судың беткі температурасы +25С-тан жоғары аймақтарында маржандық аралдар (Үлкен Аустрия Тосқауыл рифі, Маржан теңізінің аралдары) орналасқан. Аралдар жеке-дара және топ болып кездеседі, аралдар тобын архипелаг деп атайды. Жер шарындағы ірі архипелагтар қатарына Канаданың Арктикалық архипелагы, Малайя архипелагы, Шпицберген архипелагы жатады.

Құрлық материктерге бөлінумен қатар, дүние бөліктеріне де жіктеледі. Дүние бөліктері дегеніміз құрлықтың ашылуы мен қоныстану ерекшеліктеріне сәйкес шартты түрде ажыратылатын тарихи-географиялық ірі аймақтар. Дүние бөліктері де алтау: Еуропа, Азия, Африка, («Ескі дүние»), Америка, Аустралия, Антарктика («Жаңа Дүние»).

Жер шарының аса ірі материгі Еуразияны ежелгі грек географтары екі дүние бөлігіне ажыратқан. Бұл дүние бөліктері Месопотамияны мекендеген ежелгі халықтар – финикиялықтардың «эреб»-батыс, «асу»-шығыс деген сөздерінің негізінде Еуропа және Азия деп аталған. Кейінірек ашылған Солтүстік және Оңтүстік Америка материктері табиғат жағдайларының айырмашылықтарына қарамастан, біртұтас Америка дүние бөлігіне біріктірілген. Дүние бөліктерінің құрамына көршілес жатқан аралдар да енеді.

0,0(0 оценок)

Ответ:

Steyflie

03.11.2021 01:00

$h = \frac{ s }{ ( 1/ \mu - 1/ tg{\alpha} )( \cos{\alpha} - \mu \sin{\alpha} )^2 }$ , при условии: $arctg{(\mu)} < \alpha < arcCtg{(\mu)}$ ;

*** если же переход от наклонной плоскости скруглённый, и: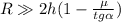 $R \gg 2h ( 1 - \frac{\mu}{tg{\alpha}} )$ , то:

$h = \frac{ s }{ 1/\mu - 1/tg{(\alpha)} }$ .

Объяснение:

По закону сохранений энергии:

$E_{ko} + E_{no} - A_\alpha = E_{k\alpha} + E_{n\alpha}$ ;

где:

$E_{ko} = 0$ и $E_{no} = mgh$ – начальные значения кинетической и потенциальной энергии;

$E_{k\alpha} = \frac{mv_\alpha^2}{2}$ и $E_{n\alpha} = 0$ – значения кинетической и потенциальной энергии перед ударом о горизонтальную поверхность, в самом низу наклонной плоскости;

$A_\alpha$ – работа силы трения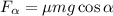 на наклонной плоскости;

$A_\alpha = F_\alpha \cdot L$ – работа

силы трения $F_\alpha = \mu mg \cos{\alpha}$ на наклонной плоскости,

где: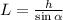 $L = \frac{h}{\sin{\alpha}}$ – длина наклонной плоскости;

$A_\alpha = \frac{ \mu mgh }{tg{\alpha}}$ ;

В итоге:

$mgh - \frac{ \mu mgh }{tg{\alpha}} = \frac{mv_\alpha^2}{2}$ ;

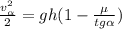(*) $\frac{v_\alpha^2}{2} = gh ( 1 - \frac{\mu}{tg{\alpha}} )$ ;

Из этого вытекает очевидное условие, что:

$1 - \frac{\mu}{tg{\alpha}} 0$ ;

$1 \frac{\mu}{tg{\alpha}}$ ;

$tg{\alpha} \mu$ , т.е. угол наклона должен быть более значения: $\alpha arctg{(\mu)}$ , иначе груз вообще не сдвинется с места, и, разумеется, никакого расстояния не пройдёт, а общая формула (данная в ответе) даст формально отрицательный ответ для высоты .

Теперь «удар», т.е. переход с наклонной плоскости на горизонталь. Во время удара теряется вертикальная составляющая импульса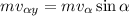 $mv_{\alpha y} = mv_\alpha \sin{\alpha}$ . Это происходит почти мгновенно ( 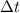$\Delta t$ ), под воздействием гасящей его чрезвычайно резко возрастающей на время гашения силы реакции опоры (и веса – соответственно) 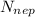$N_{nep}$ . Удар груза об опору в момент его перехода на горизонталь будем считать абсолютно неупругим, происходящим таким образом, что груз после него не подскакивает. Тогда можно записать, что:

$mv_{\alpha y} - N_{nep} \Delta t = 0$ ;

$N_{nep} = \frac{mv_{\alpha y}}{\Delta t}$ ;

За это время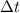 $\Delta t$ груз так же заметно замедляется под воздействием чрезвычайно резко возрастающей на время гашения силы трения:

$F_{nep} = \mu N_{nep} = \mu \cdot \frac{mv_{\alpha y}}{\Delta t}$ ;

Соответственно, гасится и горизонтальный импульс:

$mv_\alpha' = mv_{\alpha x} - F_{nep} \Delta t = mv_\alpha \cos{\alpha} - \mu \cdot \frac{mv_{\alpha y}}{\Delta t} \cdot \Delta t =$

$= mv_\alpha \cos{\alpha} - \mu mv_\alpha \sin{\alpha} = mv_\alpha ( \cos{\alpha} - \mu \sin{\alpha} )$ ;

$v_\alpha' = v_\alpha ( \cos{\alpha} - \mu \sin{\alpha} )$ ;

Из последнего вытекает очевидное условие, что:

$\cos{\alpha} - \mu \sin{\alpha} 0$ ;

$\cos{\alpha} \mu \sin{\alpha}$ ;

$\frac{\cos{\alpha}}{\sin{\alpha}} \mu$ ;

$tg{\alpha} < \frac{1}{\mu}$ , т.е. угол наклона должен быть не более определённого значения: $\alpha < arctg\frac{1}{\mu} = arcCtg{(\mu)}$ , иначе груз после удара о горизонтальную плоскость просто остановится, и никакого расстояния не пройдёт, а общая формула (данная в ответе) даст формально отрицательный ответ для высоты .

Кинетическая энергия груза после «ударного» торможения:

$E_{k\alpha}' = \frac{1}{2} mv_\alpha'^2 = \frac{1}{2} mv_\alpha^2 ( \cos{\alpha} - \mu \sin{\alpha} )^2$ ;

Далее, снова по закону сохранений энергии (с учётом неизменного значения потенциальной):

$E_{k\alpha}' - A_{ocm} = E_{k}'$ ;

где:

$A_{ocm} = F_{mp} \cdot s = \mu mg s$ – работа силы трения на горизонтальном участке до остановки;

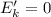а $E_{k}' = 0$ – конечная кинетическая энергия (остановка);

$\frac{1}{2} mv_\alpha^2 ( \cos{\alpha} - \mu \sin{\alpha} )^2 = \mu mg s$ ;

$\frac{v_\alpha^2}{2} = \frac{ \mu g s }{ ( \cos{\alpha} - \mu \sin{\alpha} )^2 }$ ;

Учитывая (*):

$gh ( 1 - \frac{\mu}{tg{\alpha}} ) = \frac{ \mu g s }{ ( \cos{\alpha} - \mu \sin{\alpha} )^2 }$ ;

$h ( 1 - \frac{\mu}{tg{\alpha}} ) = \frac{ \mu s }{ ( \cos{\alpha} - \mu \sin{\alpha} )^2 }$ ;

$h = \frac{ s }{ ( 1/ \mu - 1/ tg{\alpha} )( \cos{\alpha} - \mu \sin{\alpha} )^2 }$ .

*** Если же переход от наклонной плоскости гладкий, и при этом: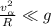 $\frac{v_\alpha^2}{R} \ll g$ , т.е. радиус перехода: 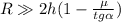$R \gg 2h ( 1 - \frac{\mu}{tg{\alpha}} )$ , то «ударная» потеря – пренебрежима, и: 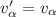$v_\alpha' = v_\alpha$ , а, значит: