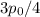Железнодорожный локомотив тянет за собой три платформы - вопрос №14689831 от KindPioneer 11.09.2020 23:40

Question

Физика: Железнодорожный локомотив тянет за собой три платформы со строительными материалами развивая силу тяги 15 тысяч Н. Массы платформ с материалами соответственно 15, 20, и 25 тон. В некоторый момент времени этот состав догнал дизельный тепловоз, который сцепился с последним вагоном и попытался остановить движущийся состав развивая силу тяги в 4 тысячи Н, приложенных в направлении обратном движению состава. Найдите силы, с которыми в этом случае натягивается сцепление между железнодорожными платформами.

KindPioneer · Answer

Разделим молекулы на две группы: те, что абсолютно упруго соударяются со стенкой, и те, что к стенке прилипают.

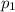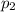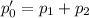Давление в первой группе $p_{1}$ , а во второй - $p_{2}$ ; Тогда $p_{0}'=p_{1}+p_{2}$ ;

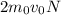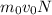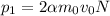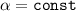Заметим, что давление пропорционально средней силе, которая оказывается молекулами на стенку сосуда, которая в свою очередь (согласно второму закону Ньютона), пропорциональна изменению импульса падающих молекул. Для первой группы изменение импульса (суммарное) равно $2m_{0}v_{0}N$ , а для второй - $m_{0}v_{0}N$ ; Тогда $p_{1}=2\alpha m_{0}v_{0}N$ , где $\alpha=\texttt{const}$ - постоянная для рассматриваемого газа. Аналогично 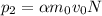$p_{2}=\alpha m_{0}v_{0}N$ ; Изначально 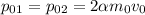$p_{01}=p_{02}=2\alpha m_{0}v_{0}$ , т.е. 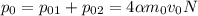$p_{0}=p_{01}+p_{02}=4\alpha m_{0}v_{0}N$ ;

А теперь: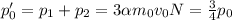 $p_{0}'=p_{1}+p_{2}=3\alpha m_{0}v_{0}N=\frac{3}{4}p_{0}$

ответ: $3p_{0}/4$