1. Чему равна сумма углов выпуклого 102-угольника?
2. Сколько сторон имеет выпуклый многоугольник, сумма углов которого равна 1260°?
3. Диагональ разбивает выпуклый шестиугольник на два многоугольника, один из которых является четырёхугольником. Определите вид другого многоугольника
4. Диагональ разбивает выпуклый n-угольник на два многоугольника, один из которых является треугольником. Определите вид другого многоугольник
5. Периметр семиугольника, все стороны которого равны, на 42 см больше его стороны. Чему равна сторона семиугольника?
6. Многоугольник разделён на три многоугольника, площади которых равны 10 кв. см, 20 кв. см и 30 кв. см. Чему равна площадь данного многоугольника?
7. Найдите площадь прямоугольника, стороны которого равны 0,8 м и 30 см.
8. Найдите неизвестную сторону прямоугольника, если его площадь и одна из сторон соответственно равны 270 кв. см и 3 дм.
9. Стороны прямоугольника равны 4 см и 9 см. Чему равна сторона равновеликого ему квадрата?
10. Верно ли утверждение? Два равновеликих прямоугольника равны.
Да
Нет
11. Верно ли утверждение? Два равновеликих квадрата равны.
Да
Нет
12. Сторона квадрата равна большей стороне прямоугольника. Какой из этих четырёхугольников имеет бóльшую площадь?
Квадрат
Прямоугольник
13. Во сколько раз надо уменьшить сторону квадрата, чтобы его площадь уменьшилась в 36 раз?
14. Как изменится площадь прямоугольника, если: каждую его сторону увеличить в 4 раза?
№1
0,25
№2
81x⁴-108x³√6+324x²-72x√6+36
№3
10
Пошаговое объяснение:
№1
0,5sin(-1650°)=-0,5sin(4*360°+210°)=-0,5sin(210°)=-0,5sin(180°+30°)=-0,5sin(-30°)=0,5*sin(30°) =0,5*0,5=0,25
№2
найдем коэффициенты бинома Ньютона из треугольника Паскаля (смотри картинку). Так как у нас 4-я степень, то коэффициенты будут 1,4,6,4,1
Получаем формулу (x+y)⁴=x⁴+4x³y+6x²y²+4xy³+y⁴
у нас x=√6, y=-3x
(√6-3x)⁴=(√6)⁴+4(√6)³*(-3x)+6(√6)²(-3x)²+4(√6)(-3x)³+(-3x)⁴=36-4*6√6*3x+6*6*9x²-4√6*27x³+81x⁴= 36-72x√6+324x²-108x³√6+81x⁴
=81x⁴-108x³√6+324x²-72x√6+36
№3
\begin{gathered}\sqrt{12+\sqrt{44} } *\sqrt{12-\sqrt{44} } = \sqrt{(12+\sqrt{44})(12-\sqrt{44}) } =\sqrt{12^2-(\sqrt{44})^2 }=\\ = \sqrt{144-44 }=\sqrt{100} =10\end{gathered}
12+
44
∗
12−
44
=
(12+
44
)(12−
44
)
=
12
2
−(
44
)
2
=
=
144−44
=
100
=10
Дано:
Усеченный конус
Sосн₁ = 9π см²
Sосн₂ = 100π см²
Sсеч = 312π см²
--------------------------------
Найти:
h - ?
1) Сначала мы найдем радиусы окружности верхнего и нижнего усеченного конуса используя площадь круга:
Sосн₁ = πr² ⇒ r = √Sосн₁/π = √9π см²/π = √9 см² = 3 см ⇒ BO₁ = BC = 3 cм
Sосн₂ = πR² ⇒ R = √Sосн₁/π = √100π см²/π = √100 см² = 10 см ⇒ AO = OD = 10 см
2) Равнобедренная трапеция ABCD является осевым сечением данного усеченного конуса: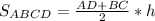
3) В трапеции ABCD:
AD = 2AO = 2R = 2×10 см = 20 см
BC = 2BO₁ = 2r = 2×3 см = 6 см
4) И теперь находим высоту равнобедренной трапеций ABCD:
ответ: h = 24 см
P.S. Рисунок показан внизу↓