1. Дан треугольник NRC. ∠ N = 12°, ∠ R = 59°. Определи величину ∠ C.
∠ C =
°.
2. Дан прямоугольный треугольник, величина одного острого угла которого составляет 47°. Определи величину второго острого угла этого треугольника.
Величина второго острого угла равна
°.
Угол САД = 180 - (угод Д + угол АСД) = 180 - (60 + 90) = 30 град
Угол ВАС = угол САД = 30 град (по условию)
Угол ВСА = угол САД = 30 град (свойства трапеции)
Следовательно угол ВАС = угол ВСА и треугольник АВС - равнобедренный
ВС = АВ = х
Угол А = угол ВАС + угол САД = 30 + 30 = 60 град
Следовательно угол А = угол Д и трапеция равнобедренная
СД = АВ = х
АД = СД / синус САД = х / синус 30 = х / (1/2) = 2х
Периметр трапеции
АВ + ВС + СД + АД = х + х + х + 2х = 35
5х = 35
х = 7
АВ = х = 7 см
Назовём данный треугольник АВС.
ВВ1- высота к АС.
АА1=СС1 - высоты к равным боковым сторонам.
Высота равнобедренного треугольника, проведенная к основанию, является его биссектрисой и медианой. ⇒
АВ1=СВ1=30:2=15 см
∆ АВВ1=∆ СВВ1 ( по трем сторонам).
Из ∆ АВВ1 по т.Пифагора
ВВ1=√(AB²-AB1²)=√(17²-15²)=8 см
Высоты к боковым сторонам найдем из площади ∆ АВС
Заметим, что ∆ АВС - тупоугольный ( АС² > АВ²+ВС²), поэтому высоты, проведенные к боковым сторонам тупоугольного треугольника, лежат вне его.
S(ABC)=BB1•AC:2=8•15=120 см²
AA1=2S(ABC):BC
AA1=CC1=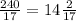 см
см