1.катет прямоугольного треугольника больше другого катета на 10 и меньше гипотенузы на 10. найти гипотенузу 2.меньшая сторона прямоугольника равна 4 , а угол между диагоналями равен 120. найти площадь прямоугольника
2. Разделим получившийся треугольник с вершиной с углом 120 градусов высотой на два треугольника. Получим прямоугольный треугольник с катетами, равными половинам сторон прямоугольника. При этом известна длина меньшего катета: 4/2=2 и примыкающий угол а=120/2=60 градусов. Больший катет равен:
1. Катет 1 - длина х
катет 2 - длина (x-10)
гипотенуза - длина (х+10)
Правило прямоугольного треугольника:
х^2 + (x-10)^2 = (x+10)^2
x^2 + x^2 - 2*10*x + 100 = x^2 + 2*10*x + 100
2x^2 - 20x=x^2 + 20x
2x-20 = x+20
x=40
Катет 1 = 40, катет 2 = 30, гипотенуза = 50.
2. Разделим получившийся треугольник с вершиной с углом 120 градусов высотой на два треугольника. Получим прямоугольный треугольник с катетами, равными половинам сторон прямоугольника. При этом известна длина меньшего катета: 4/2=2 и примыкающий угол а=120/2=60 градусов. Больший катет равен:
2*tg60=2*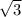
Площадь прямоугольника: 4*2*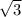 = 8*
= 8*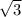
ответ: 8*