1)Медиана КР треугольника КНТ равна половине стороны НТ. Докажите, что ⊿КНТ прямоугольный. 2) Внутри отрезка AB взяли произвольную точку M. Точка C – середина отрезка AM, а точка D – середина отрезка MB. А точка P – середина отрезка CM, а точка Q – середина отрезка MD. Найдите длину отрезка PQ, если длина отрезка AB равна 40 сантиметрам.

Прямые KC и AD являются скрещивающимися, то есть не лежат в одной плоскости. Но известно, что в качестве угла между скрещивающимися прямыми a и b надо брать меньший из четырех углов пресекающихся прямых a и c, где прямая c параллельна прямой b.  В нашем случае в качестве прямой c надо взять прямую BC.

Итак, искомый угол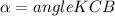

При этом Угол KCB найдем по свойству внутренних углов треугольника:

        угол KCB= 180 градусов - (угол KBC + угол BKC)=180 - (100+32)= 48 градусов 

Таким образом,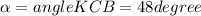

  где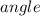 - угол 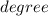- градус

Эта задача очень легко решается,я вложила фото с решением внизу

Чтобы решить задачу тебе надо:

1.Начертить рисунок(см.фото)

2.Написать дано(всё,что известно в задаче)

3.Начать решать

Для начала найдём угол В .Нам известно,что угол DBC равен 130 градусам ,а угол В смежный с ним ,значит угол В равен 180 градусов (сумма смежных углов равна 180 градусов) минус 130 градусов = 50 градусов.Из задачи мы знаем,что угол В равен углу А,это значит,что угол Ф тоже равен 50 градусов.Осталось найти угол С.Из теоремы мы знаем ,что сумма углов треугольника равна 180 градусов ,значит угол С равен 180 градусов минус сумма углов А и В.Мы получим ответ : угол С равен 80 градусов.