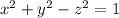 , проходящих через точку M(1; 1; 1). 2) Составить уравнение эллиптического параболоида, имеющего вершину в начале координат, осью которого является ось Oz, если на его поверхности заданы две точки M(-1;-2;2) и N(1;1;1).
, проходящих через точку M(1; 1; 1). 2) Составить уравнение эллиптического параболоида, имеющего вершину в начале координат, осью которого является ось Oz, если на его поверхности заданы две точки M(-1;-2;2) и N(1;1;1).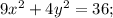 2.
2. 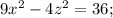 3.
3. 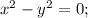 4.
4. 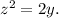
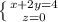 вокруг оси Oy.
вокруг оси Oy.
Обозначим вершины трапеции АВСD. Стороны: АВ=15, ВС=16, СD=20, AD=41. Из вершины С проведем СК параллельно АВ. Тогда АВСК - параллелограмм, и СК=15 см, АК=ВС=16 см, КD=AD-AK=25 см. Отношение сторон ∆ СКD=15:20:25, т.е. 3:4:5. ⇒ ∆ КСD - так называемый египетский, он прямоугольный. Площадь ∆ КСD=KC•CD:2=150 см². Тогда его высота СН=2S:KD=300:25=12 см (она же высота трапеции АВСD). Площадь трапеции равна половине произведения высоты на сумму оснований. S(ABCD)=CH•(BC+AD):2=12•57:2=342 см²
Подобных задач с полным и правильным ответом на сайте немало. При желании можно найти другие варианты решения.
В треугольнике АВ1А1 по теореме Менелая:
(ВС1/С1А)*(АР/РА1)*(А1С/СВ) = 1. Подставим известные соотношения: ВС1/С1А = 1/1 (СС1 - медиана), СА1/ВС=1/3 (СА1/А1В=1/2 - дано ). Тогда (1/1)*(АР/РА1)*(3/1) =1 => АР/РА1 = 3/1.
ответ: медиана СС1 делит отрезок АА1 в отношении АР:РА1 = 3:1.
Без применения формулы Менелая.
Проведем С1К параллельно ВС. С1К - средняя линия треугольника АВА1, так как точка С1 делит сторону АВ пополам, а отрезок КС1 параллелен стороне ВС по построению. Треугольники АС1К и АВА1 подобны с коэффициентом k=1/2. АК=КА1. Треугольники РС1К и РСА1 подобны с коэффициентом k=1/1 (то есть равны, так как СК=(1/2)*ВА1). КР=РА1.Тогда АР = 3*РА1. То есть отношение АР/РА1 = 3:1.