1.Площади оснований усеченного конуса равны 9пи см2 и 49пи см2.
Найдите площадь сечения, параллельного плоскостям оснований
и проходящего через середину высоты конуса.

2.Высота конуса равна Н. Найдите образующую и радиус осно-
вания конуса, если образующая наклонена к плоскости основания
под углом а

Показать ответ

Ответ:

redf0x0

08.02.2023 03:45

На рисунке изображен график линейной функции. Напишите формулу, которая задает линейную функцию

. Уравнение прямой в отрезках

Уравнение прямой в отрезках на плоскости в прямоугольной системе координат Oxy имеет вид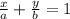 $\frac{x}{a} +\frac{y}{b} =1$ где a и b - некоторые отличные от нуля действительные числа , при чем | a| и |b| равны длинам отрезков, которые отсекает прямая на координатных осях Ox и Oy, считая от начала координат.

$\frac{x}{-4} +\frac{y}{4} =1 |*4\\-x+y=4\\y=x+4$

. Через координаты 2-х точек.

Уравнение прямой у=кх+в.

Точка пересечения с Оу имеет координаты ( 0; 4)⇒ 4= к*0+в ,в=4

Точка пересечения с Ох имеет координаты (-4; 0) ⇒ 0=к*(-4)+в или

0=-4к+4 , к=1.

Уравнение прямой у=х+4.

0,0(0 оценок)

Ответ:

STONEISLAND1488

01.06.2023 08:17

S = 24 cм².

Объяснение:

Пирамида правильная, следовательно, основания - правильные треугольники. По формулам радиусы описанных окружностей этих треугольников равны: ОС = R = (√3/3)·а = 8√3/3 см, аналогично,

R1 = 5√3/3 см. Радиус вписанной окружности r = OH = R/2 = 4√3/3 см.

Тогда ОР = ОН +ОР = 4√3/3 + 5√3/3 = 9√3/3 = 3√3 см. (так как ОР = О1С1).

В прямоугольном треугольнике С1НР по Пифагору найдем С1Н - высоту сечения АВС1 (по теореме о трех перпендикулярах).

С1Н = √(НР²+С1Р²) = √(27+9) = 6 см.

Площадь сечения (треугольника АВС1) равна:

S = (1/2)·AB·C1H = (1/2)·8·6 = 24 cм².