1.Верно ли, что две прямые, перпендикулярные некоторой плоскости, лежат в одной
плоскости?
2.Могут ли два боковых ребра пирамиды быть перпендикулярными плоскости основания
пирамиды?
3.Можно ли провести прямую, перпендикулярную двум пересекающимся плоскостям?
4.Существует ли взаимосвязь между расположением ножек стола относительно его
поверхности и пола, на котором он стоит?
5.Существует ли сечение куба плоскостью, перпендикулярной ровно двум его рёбрам?
6.Можно ли провести плоскость, перпендикулярную одновременно двум скрещивающимся
прямым?
7.Почему ледовые сосульки, свисающие с крыши весной, можно считать параллельными
между собой (пренебрегая их толщиной)?
8.На потолке закреплен крюк. С канатов необходимо подвесить к нему платформу
так, чтобы ее плоскость была горизонтальной. Как это сделать?
9.Можно ли через данную точку провести три взаимно перпендикулярные
прямые? А четыре?
10.Сколько различных плоскостей определяют четыре прямые, перпендикулярные одной
плоскости?

Показать ответ

Ответ:

puh9999

27.03.2021 01:47

Дано:
треугольник АВС
АB = BC
AC - основание
угол ВАС = угол АСВ = 70°
АE - бисс. угла ВАС
СE - бисс. угла ВСА
Найти: углы треугольника АЕС
Решение:
1. Так как АЕ - бисс. угла ВАС, то угол ВАЕ = угол ЕАС. Так как СЕ - бисс. угла ВСА, то угол ВСЕ = угол ЕСА
2. угол ВАЕ + угол ЕАС = угол ВАС
угол ЕАС = 70° / 2 = 35°
3. угол ЕАС = угол ЕСА = 35° (СЕ и АЕ - это бисс. одинаковых углов)
4. угол АЕС + угол ЕАС + угол ЕСА = 180°
угол АЕС = 180° - 35° - 35° = 110°
ответ: угол АЕС = 110°, угол ЕАС = 35°, угол ЕСА = 35°.

0,0(0 оценок)

Ответ:

ABAYMALGAZHDAROvvv

13.08.2021 08:17

Дано: пирамида SABC, SH⊥(ABC), SH = 4 см,

∠ASH=∠CSH=∠BSH=45°, ∠ACB=90°, ∠BAC=30°

Найти : Sбок

Решение : так как боковые рёбра образуют с высотой пирамиды равные углы, значит, они образуют равные углы с основанием пирамиды (острые углы прямоугольных треугольников, равных по общему катету и острому углу). ⇒ Высота опускается в центр окружности, описанной около основания пирамиды. Основание пирамиды - прямоугольный треугольник, центр описанной окружности лежит на середине гипотенузы. H ∈ AB, AH = BH.

SH⊥(ABC) ⇒ SH⊥AB ⇒ ∠SHA=90°

ΔSAH - прямоугольный равнобедренный, так как ∠SAH=∠ASH=45° ⇒ AH = SH = 4 см ⇒ AB = AH + BH = 8 см; SA = 4√2 см

SA = SB = SC = 4√2 см

ΔABC - прямоугольный. Катет, лежащий против угла 30°, равен половине гипотенузы. BC = AB/2 = 4 см

По теореме Пифагора

AC² = AB² - BC² = 8² - 4² = 48

AC = √48 = 4√3 см

$S_{\Delta ASB}=\dfrac{AB\cdot SH}2=\dfrac {8\cdot 4}2=16$ см²

Площадь двух других граней можно найти по формуле Герона

$S=\sqrt{p(p-a)(p-b)(p-c)}$

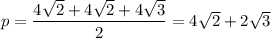
ΔASC, $p=\dfrac{4\sqrt2+4\sqrt2+4\sqrt3}2=4\sqrt2+2\sqrt3$

$S_{\Delta ASC}=\sqrt{(4\sqrt2+2\sqrt3)(4\sqrt2+2\sqrt3-4\sqrt2)(4\sqrt2+2\sqrt3-4\sqrt2)(4\sqrt2+2\sqrt3-4\sqrt3)}=\\\\=\sqrt{(4\sqrt2+2\sqrt3)(2\sqrt3)(2\sqrt3)(4\sqrt2-2\sqrt3)}=\sqrt{(32-12)\cdot 12}=\sqrt{240}\boldsymbol{=4\sqrt{15}}$

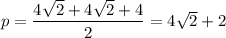
ΔBSC, $p=\dfrac{4\sqrt2+4\sqrt2+4}2=4\sqrt2+2$

$S_{\Delta BSC}=\sqrt{(4\sqrt2+2)(4\sqrt2+2-4\sqrt2)(4\sqrt2+2-4\sqrt2)(4\sqrt2+2-4)}=\\\\=\sqrt{(4\sqrt2+2)\cdot2\cdot2(4\sqrt2-2)}=\sqrt{(32-4)\cdot 4}=\sqrt{28\cdot 4}\boldsymbol{=4\sqrt{7}}$