2. На рисунке прямые d и f, а так же прямые f и h параллельны. Определите градусную меру /_2 и /_3, если /_1 = 24°

2. На рисунке прямые d и f, а так же прямые f и h параллельны. Определите градусную меру /_2 и /_3,

Показать ответ

Ответ:

nastusya1709

06.03.2021 07:35

По второму признаку равенства треугольников: "Если сторона и два прилежащих к ней угла в одном треугольнике равны стороне и двум прилежащим к ней углам во втором треугольнике - то такие треугольники равны".
Нам дано, что BM - биссектриса (на рисунке) , значит угол ABM равен углу CBM по определению биссектрисы
Она же есть высота. По определению высоты BM перпендикулярна AC, значит углы AMB и CMB равны между собой (каждый по 90 градусов)
А также сторона BM - общая для треугольников ABM и CBM, значит эти два треугольника равны по 2-му признаку равенства треугольников.
В равных треугольниках против равных углов лежат равные стороны (и наоборот) . Прямые углы AMB и CMB равны, значит и стороны, лежащие против них AB и CB. По определению, треугольник, у которого две стороны равны, называется равнобедренным.
Утверждение доказано.
Докажите, что если биссектриса треугольника является высотой, то треугольник - равнобедренный

Докажите, что если биссектриса треугольника является высотой, то треугольник - равнобедренный

0,0(0 оценок)

Ответ:

Машуничка12

16.10.2021 22:33

$15\sqrt{5}$ (кв. единица)

Объяснение:

По условию задано координаты трёх его вершин параллелограмма АВСD: А(27;18;20) , В(24;18;16) и С(18;21;18). Так как верно свойство (см. рисунок) "Диагональ параллелограмма делит его на два равных треугольника", то площадь параллелограмма S(ABCD) равна удвоенной площади одного из треугольников, то есть

S(ABCD)=2·S(ABC).

В нашем случае диагональ AC делит параллелограмм на два равных треугольника. Поэтому достаточно найти площадь S(ABC) треугольника ABC по формуле Герона:

$\tt \displaystyle S(ABC)=\sqrt{p \cdot (p-a) \cdot (p-b) \cdot(p-c) },$

где p - полупериметр: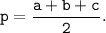 $\tt \displaystyle p=\frac{a+b+c}{2} .$

Стороны треугольника ABC находим по формуле расстояния между двумя точками с координатами M(x₁; y₁; z₁) и N(x₂; y₂; z₂):

$\tt \displaystyle d(MN)=\sqrt{(x_{1} -x_{2} )^{2}+(y_{1} -y_{2} )^{2}+(z_{1} -z_{2} )^{2}} .$

Так как А(27;18;20), В(24;18;16) и С(18;21;18), то

$\tt \displaystyle a=d(AB)=\sqrt{(27-24 )^{2}+(18 -18)^{2}+(20 -16 )^{2}} =\\\\=\sqrt{3^{2}+0^{2}+4^{2}} =\sqrt{9+16} =\sqrt{25} =5;$

$\tt \displaystyle b=d(BC)=\sqrt{(24-18 )^{2}+(18-21)^{2}+(16-18)^{2}} =\\\\=\sqrt{6^{2}+3^{2}+2^{2}} =\sqrt{36+9+4} =\sqrt{49} =7;$

$\tt \displaystyle c=d(AC)=\sqrt{(27-18 )^{2}+(18-21)^{2}+(20-18)^{2}} =\\\\=\sqrt{9^{2}+3^{2}+2^{2}} =\sqrt{81+9+4} =\sqrt{94};$

$\tt \displaystyle p=\frac{5+7+\sqrt{94}}{2}= \frac{12+\sqrt{94}}{2};$

$\tt \displaystyle S(ABC)=\sqrt{\frac{12+\sqrt{94}}{2} \cdot (\frac{12+\sqrt{94}}{2}-5) \cdot (\frac{12+\sqrt{94}}{2}-7) \cdot(\frac{12+\sqrt{94}}{2}-\sqrt{94} ) }=\\\\=\sqrt{\frac{12+\sqrt{94}}{2} \cdot \frac{2+\sqrt{94}}{2} \cdot \frac{-2+\sqrt{94}}{2} \cdot \frac{12-\sqrt{94}}{2}}=\\\\=\sqrt{\frac{144-94}{4} \cdot \frac{-4+94}{4} }=\sqrt{\frac{50}{4} \cdot \frac{90}{4} }=\frac{\sqrt{25\cdot 45}}{\sqrt{2^2} } =\frac{\sqrt{5^2\cdot 3^2\cdot 5}}{2} =\frac{15\cdot\sqrt{5}}{2};$