3. _AOB=100°, 2AOK=50°, MOB=20° болатындай, «AOB-ны және ОК мен ОМ сәулелерін салыңыз. «КОМ-ның градустық шамасын табыңыз.

Дано:

ABCDEFGH - прямоугольный параллелепипед

AB:BC:BF = 1:2:3

Sполн = 550 см²

------------------------------------------------------------------------------

Найти:

AB - ?,  BC - ?,   BF - ?

Пусть AB = x см, тогда BC = 2x см, и BF = 3x см.

Запишем формулу площади полной поверхности параллелепипеда:

Sполн =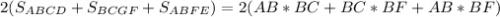

Именно по такой формуле площади полной поверхности параллелепипеда мы найдем все длины параллелепипеда:

Sполн = 2(AB×BC+BC×BF+AB×BF)

550 = 2(x × 2x + 2x × 3x + x × 3x см)

550 = 2(2x² + 6x² + 3x²)

550 = 2×11x²

550 = 22x²

x² = 25

x = √25

x = 5 см ⇒ AB = 5 см, следовательно:

BC = 2x = 2×5 см = 10 см

BF = 3x = 3×5 см = 15 см

ответ: AB = 5 см, BC = 10 см, BF = 15 см

P.S. Рисунок показан внизу↓

ответ:А (-1, -1, -1),   В (-1, 3, -1),   С (-1, -1, 2)

AB=\sqrt{\big(x_B-x_A\big)^2+\big(y_B-y_A\big)^2+\big(z_B-z_A\big)^2}==\sqrt{\big(-1-(-1)\big)^2+\big(3-(-1)\big)^2+\big(-1-(-1)\big)^2}==\sqrt{0+4^2+0}=4

CB=\sqrt{\big(x_B-x_C\Big)^2+\big(y_B-y_C\big)^2+\big(z_B-z_C\big)^2}==\sqrt{\big(-1-(-1)\big)^2+\big(3-(-1)\big)^2+\big(-1-2\big)^2}==\sqrt{0+16+9}=5

AC=\sqrt{\big(x_C-x_A\big)^2+\big(y_C-y_A\big)^2+\big(z_C-z_A\big)^2}==\sqrt{\big(-1-(-1)\big)^2+\big(-1-(-1)\big)^2+\big(2-(-1)\big)^2}==\sqrt{0+0+3^2}=3

P_{\Delta ABC}=AB+CB+AC=4+5+3=12boxed{\boldsymbol{P_{\Delta ABC}=12}}

Объяснение: