9. В треугольнике ABC из вершин А и В проведены биссектрисы. Точка пере- сечения биссектрис обозначена буквой D. Найдите угол ADB, если угол A=50°,
угол В=50°​

Пусть диагонали ромба пересекаются в точке О: АС ∩ ВD = О, диагонали ромба относятся как 3:4 ⇒ половины диагоналей ромба также относятся как 3:4 ⇒ можно обозначить: АО = 4х, ОВ = 3х. Периметр ромба равен 40 ⇒ его сторона равна 40 : 4 = 10,

АВ = ВС = СD = DА = 10. По теореме Пифагора:

АВ² = АО² + ВО² =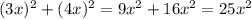 = 10² = 100 ⇒

x² = 100 : 25 = 4 ⇒ x = 2 ⇒ АО = 4х = 4*2 = 8, ОВ = 3х = 3*2 = 6,

AC = 2AO = 2*8 = 16, ВD = 2ОВ = 2*6 = 12. Площадь ромба равна:

S = 0,5 * AC * ВD = BH * AD ⇒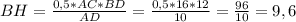

ответ: высота ромба ВН равна 9,6

Объяснение:

1

Рассмотрим тр-к АВС

По теореме Пифагора :

АВ=корень (АС^2+ВС^2)=

=корень (24^2+32^2)=корень 1600=40 мм

СD=AD=BD=AB:2=40:2=20 мм

Тр-к КСD:

По теореме Пифагора :

КD=корень (КС^2+СD^2)=

=корень (48^2+20^2)=корень 2704=

=52 мм

2

А) АК _|_ МК - НЕТ (т. к <МКА=60 градусов)

Б) тр-к АКС - прямоугольный - ДА(т. к <АКС=90 градусов)

В) тр-к МАК - равносторонний - ДА (т. к

КА=КМ, значит тр-к АКМ-равнобедренный, т. к <МКА=60 градусов <КАМ=<КМА=(180-<МКА)/2=

=(180-60)/2=60 градусов, значит тр-к

МАК- равносторонний

Г) МК_|_(АКС) - ДА

Д) тр-к МАС - прямоугольный - НЕТ

ответ : Б) ; В) ; Г)