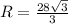Задача решается двумя Графически и алгебраически. приложение №1): Через точку С проводим диаметр окружности. Обозначаем его СМ. Проводим отрезок АМ. В треугольнике АМС угол А прямой (МС диаметр вписанного прямоугольного треугольника). АВДМ - трапеция (АМ||ВД), углы АВМ и АДМ равны (опираются на одну хорду АМ). Трапеция АВДМ - равнобедренная, АВ=МД=3 см. Треугольник МСД прямоугольный. МД=3 см, ДС=4 см, МС=√(3³+4³)=5 см. Радиус 5/2=2,5 см.
приложение №2): Радиус описанной окружности вокруг четырехугольника, равен радиусу описанной окружности любого треугольника, образованного сторонами этого четырехугольника. Радиус описанной окружности - R=a/2sinα , где а - сторона треугольника, α - противолежащий угол. Рассматриваем треугольник НВС, где Н точка пресечения диагоналей. Прямоугольный, угол Н (по условию), угол В - β, угол С - (90-β). R=СД/2sinβ=2/sinβ; R=АВ/2sin(90-β)=3/2cosβ. Делим одно выражение на другое. 3/2cosβ * sinβ/2=3tgβ/4=1, tgβ=4/3 R=2/sin(atgβ)=2.499999=2.5 см.
Нарисовал чертеж с обозначениями. Во-первых, описать окружность можно только около равнобедренной трапеции. Надо найти радиус этой окружности. Заметим, что окружность эта описана как около трапеции ABCD, так и около треугольника ABD.
Для треугольника ABD воспользуемся теоремой синусов и получим
То есть
Даже вот так. Радиус этой окружности равен длине стороны BD.
Осталось лишь её найти. Раз трапеция равнобедренная, то и прямоугольные треугольники ABH и DCK равны (по катету - высоте и гипотенузе - боковой стороне трапеции). Значит, AH = KD
Тогда AD = AH + HK + KD = 2*AH + HK
BCKH - прямоугольник, BC = HK = 12
AH = 0.5 * (AD - HK) = 0.5 * (20 - 12) = 4
HD = HK + KD = 12 + 4 = 16
Не хватает стороны BH. Её можно найти из треугольника ABH
приложение №1):
Через точку С проводим диаметр окружности. Обозначаем его СМ. Проводим отрезок АМ. В треугольнике АМС угол А прямой (МС диаметр вписанного прямоугольного треугольника). АВДМ - трапеция (АМ||ВД), углы АВМ и АДМ равны (опираются на одну хорду АМ). Трапеция АВДМ - равнобедренная, АВ=МД=3 см.
Треугольник МСД прямоугольный. МД=3 см, ДС=4 см, МС=√(3³+4³)=5 см.
Радиус 5/2=2,5 см.
приложение №2):
Радиус описанной окружности вокруг четырехугольника, равен радиусу описанной окружности любого треугольника, образованного сторонами этого четырехугольника.
Радиус описанной окружности -
R=a/2sinα , где а - сторона треугольника, α - противолежащий угол.
Рассматриваем треугольник НВС, где Н точка пресечения диагоналей.
Прямоугольный, угол Н (по условию), угол В - β, угол С - (90-β).
R=СД/2sinβ=2/sinβ;
R=АВ/2sin(90-β)=3/2cosβ.
Делим одно выражение на другое.
3/2cosβ * sinβ/2=3tgβ/4=1, tgβ=4/3
R=2/sin(atgβ)=2.499999=2.5 см.
Нарисовал чертеж с обозначениями. Во-первых, описать окружность можно только около равнобедренной трапеции. Надо найти радиус этой окружности. Заметим, что окружность эта описана как около трапеции ABCD, так и около треугольника ABD.
Для треугольника ABD воспользуемся теоремой синусов и получим
То есть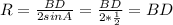
Даже вот так. Радиус этой окружности равен длине стороны BD.
Осталось лишь её найти. Раз трапеция равнобедренная, то и прямоугольные треугольники ABH и DCK равны (по катету - высоте и гипотенузе - боковой стороне трапеции). Значит, AH = KD
Тогда AD = AH + HK + KD = 2*AH + HK
BCKH - прямоугольник, BC = HK = 12
AH = 0.5 * (AD - HK) = 0.5 * (20 - 12) = 4
HD = HK + KD = 12 + 4 = 16
Не хватает стороны BH. Её можно найти из треугольника ABH
Теперь по теореме Пифагора ищем BD
ответ: