АВ және СD кесінділері әрқайсысының ортасы болатын О кимлысады. ◇АОС = ◇BOD теңдігі орындала ма? Бұл есеп шартындағы өзге де тең үшбүрыштар жұбын керестіңдер.
Т.к. трапеция равнобедренная, то уголД=углуА=60град. Проведём высоту ВН. Получаем прямоугольный треугольник АВН. Сумма углов треугольника равна 180 градусам. находим угол АВН=180-90-60=30. Катет, лежащий против угла 30град. равен половине гипотенузы. В данном случае против угла 30град. лежит АН. АН=0,5АВ=0,5*12=6. Проведем ещё одну высоту СК. Получается прямоугольный треугольник СКД. Т.к. трапеция равнобедренная, то треугольникАВН=треугольникуСКД =>АН=КД=6. Основание АД=АН+НК+КД. НК=10, т.к. ВСКН-прямоугольник. Отсюда получаем: АД=6+10+6=22.
Рассмотрим треугольник с основанием c, боковыми сторонами a и b, и медианой к основанию m. Обозначим угол наклона медианы к основанию со стороны a, и со стороны b.
По теореме косинусов:
То есть
Предположим от противного, что медиана к основанию равна полусумме боковых сторон:
Подставив выражение для в предыдущее равенство, получим:
То есть сумма двух сторон треугольника равна его третьей стороне.
Поскольку такого треугольника не существует, следовательно исходное предположение неверно, и медиана к одной стороне треугольника не может равняться полусумме двух других его сторон.
Т.к. трапеция равнобедренная, то уголД=углуА=60град. Проведём высоту ВН. Получаем прямоугольный треугольник АВН. Сумма углов треугольника равна 180 градусам. находим угол АВН=180-90-60=30. Катет, лежащий против угла 30град. равен половине гипотенузы. В данном случае против угла 30град. лежит АН. АН=0,5АВ=0,5*12=6. Проведем ещё одну высоту СК. Получается прямоугольный треугольник СКД. Т.к. трапеция равнобедренная, то треугольникАВН=треугольникуСКД =>АН=КД=6. Основание АД=АН+НК+КД. НК=10, т.к. ВСКН-прямоугольник. Отсюда получаем: АД=6+10+6=22.
Рассмотрим треугольник с основанием c, боковыми сторонами a и b, и медианой к основанию m. Обозначим угол наклона медианы к основанию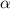 со стороны a, и
со стороны a, и 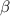 со стороны b.
со стороны b.
По теореме косинусов:
То есть
Предположим от противного, что медиана к основанию равна полусумме боковых сторон:
Подставив выражение для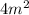 в предыдущее равенство, получим:
в предыдущее равенство, получим:
То есть сумма двух сторон треугольника равна его третьей стороне.
Поскольку такого треугольника не существует, следовательно исходное предположение неверно, и медиана к одной стороне треугольника не может равняться полусумме двух других его сторон.