1) катет, лежащий напротив угла 30°, равен половине гипотенузы.
х=18/2=9
ответ: 9
14) катет, лежащий напротив угла 30°, равен половине гипотенузы.
х=2×5=10
ответ: х=10
15) катет, лежащий напротив угла 30°,равен половине гипотенузы.
По рисунку видно, что катет меньше гипотенузы в 2 раза, значит катет длиной 4,2 лежит напротив угла 30°. Так как треугольник прямоугольный, то второй неизвестный угол равен 60°
16) Рассмотрим прямоугольный треугольник АСЕ, где угол Н равен 60°, соответственно, угол А равен 30°.
Катет лежащий напротив угла 30° равен половине гипотенузы, соотвественно, АЕ равна 14. Найдем катет АС в треугольнике АСЕ по теореме Пифагора:
АС²=14²-7² => АС= 7√3
Рассмотрим треугольник АВС:
АС лежит напротив угла 30°, соответственно, ВА = 2×7√3 = 14√3.
Проведём от точки N к точке P отрезок PN и от точки M к точке O отрезок MO так, что MN - часть средней линии данной трапеции. Соответственно, исходя из этого условия и зная длины BC и AD найдём длину отрезка PO.
(см).
Вернёмся к условию задачи. M и N — СЕРЕДИННЫЕ точки диагоналей AC и BD трапеции ABCD. И следовательно из ранее сказанной записи "MN - часть средней линии данной трапеции" мы можем сказать, что PN и MO равны сумме BC.
(см).
Поскольку нам известен отрезок, на котором находится искомый отрезок MN и два составляющих по бокам отрезка PO, то найдём отрезок MN.
Отметим, что все треугольники –прямоугольные
1) катет, лежащий напротив угла 30°, равен половине гипотенузы.
х=18/2=9
ответ: 9
14) катет, лежащий напротив угла 30°, равен половине гипотенузы.
х=2×5=10
ответ: х=10
15) катет, лежащий напротив угла 30°,равен половине гипотенузы.
По рисунку видно, что катет меньше гипотенузы в 2 раза, значит катет длиной 4,2 лежит напротив угла 30°. Так как треугольник прямоугольный, то второй неизвестный угол равен 60°
16) Рассмотрим прямоугольный треугольник АСЕ, где угол Н равен 60°, соответственно, угол А равен 30°.
Катет лежащий напротив угла 30° равен половине гипотенузы, соотвественно, АЕ равна 14. Найдем катет АС в треугольнике АСЕ по теореме Пифагора:
АС²=14²-7² => АС= 7√3
Рассмотрим треугольник АВС:
АС лежит напротив угла 30°, соответственно, ВА = 2×7√3 = 14√3.
Найдем длину ВС по теореме Пифагора:
ВС²=(14√3)²-(7√3)² => ВС =21
Найдем ВЕ:
ВЕ=21-7=14
ответ: ВЕ=14
Проведём от точки N к точке P отрезок PN и от точки M к точке O отрезок MO так, что MN - часть средней линии данной трапеции. Соответственно, исходя из этого условия и зная длины BC и AD найдём длину отрезка PO.
Вернёмся к условию задачи. M и N — СЕРЕДИННЫЕ точки диагоналей AC и BD трапеции ABCD. И следовательно из ранее сказанной записи "MN - часть средней линии данной трапеции" мы можем сказать, что PN и MO равны сумме BC.
Поскольку нам известен отрезок, на котором находится искомый отрезок MN и два составляющих по бокам отрезка PO, то найдём отрезок MN.
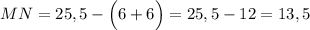 (см)
(см)
ответ: