Через концы отрезка MN и его
середину К проведены
параллельные прямые,
пересекающие плоскость α в точках
M 1, , N1 и К1 . Найдите длину отрезка
КК1 , если отрезок MN не пересекает α и
ММ1 = 12см, NN1= 4 см.

Показать ответ

Ответ:

Sofi432432

21.09.2022 05:07

Сделаем рисунок к задаче.

Продлим сторону АD и проведем к ней перпендикуляр СН1=СН,

так как АD параллельна ВС, а отрезки перпендикуляров между параллельными прямыми равны.
АН1=АD+DН1

Рассмотрим прямоугольный треугольник АСН1

Гипотенуза АС=10
Катет СН1=6

Найдем АН1 по теореме Пифагора
АН1²=АС²-ВН1²
АН1²=100-36=64
АН1=8

Площадь ромба АВСD равна произведению высоты ВН на сторону ромба.

Высота известна, сторону ромба предстоит найти.
Рассмотрим треугольник DВН1
В нем катет СН1 =6

Пусть гипотенуза СD=х,
АD=DС=х
тогда катет DH1= АН1-АD=8-х, так как АН1=АD+DН1=8, как найдено выше.
h²=х²-(АН1-х)²
36=х²-(8-х)²
36=х²-(64-16х+х²)
36=х²- 64+16х-х²)
36=-64+16х
16х=100
х=6,25
AD=6,25
Sромба=АD*h=6,25·6=37,5 см²

Есть ромб его большая диагональ 10 см а высота 6 см найти площадь ромба

0,0(0 оценок)

Ответ:

jenek28022008

06.03.2020 09:12

Формула длины дуги сектора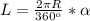 $L= \frac{2 \pi R}{360^o } * \alpha$

т.е. длина окружности делится на ее градусную меру и умножается на величину угла сектора.

По условию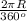 $\frac{2 \pi R}{360^o}$ •α=2π, откуда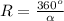 $R= \frac{360^o}{ \alpha }$

Формула площади кругового сектора S=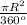 $\frac{ \pi R^2}{360^o}$ •α, т.е. площадь полного круга делится на его градусную меру и умножается на градусную меру сектора.

Подставим в формулу площади найденное из длины дуги значение R:

$R= \frac{ \pi 360^o*360^o}{ \alpha^2*360^o} * \alpha= \frac{ \pi 360^o} \alpha$

По условию π•360°/α=6π ⇒

α=60°⇒ R=360°:60°=6 см

Проведем биссектрису ОН угла сектора и к точке её пересечения с окружностью проведем касательную . Продлим стороны угла сектора до пересечения с касательной в т.А и В.

∆ АОВ - равносторонний с высотой ОН=R=6

Радиус вписанной в правильный треугольник окружности равен 1/3 его высоты.

r=6:3=2

C=2πr=4π