Окружность, центр которой расположен в первой координатной четверти, касается оси Ox в точке M, пересекает две гиперболы y = и y = (k1, k2 > 0) в точках A и B таких, что прямая AB проходит через начало координат O. Известно, что k1 * k2 = 144. Найдите наименьшую возможную длину отрезка OM.В ответ запишите квадрат длины ОМ.
Объяснение:
Прямая АВ , проходящая через начало координат имеет вид у=кх
Найдем точки пересечения этой прямой и гипербол:
y = и у=кх → = кх , х²= ; x = ( т.к. точка пересечения в 1 четверти , то х>0 ). Тогда у= к* .
y = и у=кх → = кх , х²= ; x = ( т.к. точка пересечения в 1 четверти , то х>0 ). Тогда у= к* .
По свойство касательной и секущей проведенных из одной точки ОМ²=ОА*ОВ. Найдем ОА и ОВ по формулам расстояния между точками : ОА= = ,
ОB= = .
Тогда ОМ²= * = . Т.к ≥2 ,по следствию из неравенства о среднем арифметическом и среднем геометрическом , то принимает наименьшее значение равное 2 , а к1*к2=144, то ОМ²=2*√144=2*12=24.
===========================================
Свойство касательной и секущей проведенных из одной точки : "Если из точки к окружности проведены касательная и секущая, то квадрат отрезка касательной от данной точки до точки касания равен произведению длин отрезков секущей от данной точки до точек её пересечения с окружностью."
Формула расстояния между точками d=√( (х₁-х₂)²+(у₁-у₂)² ), где (х₁;у₁ ), (х₂;у₂ ) -координаты концов отрезка.
Если прямая (DC), параллельна какой-нибудь прямой (AB), расположенной в плоскости (α), то она параллельна самой плоскости. Если плоскость проходит через прямую (DC), параллельную другой плоскости (α), и пересекает эту плоскость, то линия пересечения (EF) параллельна первой прямой (DC). Расстояние от прямой DC до плоскости α - это перпендикуляр из любой точки этой прямой на плоскость α. Итак, в прямоугольном треугольнике АЕD катет АЕ равен по Пифагору АЕ=√(AD²-DE²)=√(36²-18²)=18√3. Угол между двумя пересекающимися плоскостями равен углу между прямыми, по которым они пересекаются с любой плоскостью, перпендикулярной их линии пересечения. То есть угол между плоскостью α и плоскостью квадрата - это угол EAD, cинус которого равен отношению противолежащего катета к гипотенузе: Sinβ=ED/AD=18/36=1/2. Значит угол между плоскостями равен 30°. Площадь проекции квадрата на плоскость α - это площадь прямоугольника AEFB, равная S=AB*AE=36*18√3=648√3см²
Окружность, центр которой расположен в первой координатной четверти, касается оси Ox в точке M, пересекает две гиперболы y =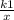
и y = 
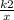(k1, k2 > 0) в точках A и B таких, что прямая AB проходит через начало координат O. Известно, что k1 * k2 = 144. Найдите наименьшую возможную длину отрезка OM.В ответ запишите квадрат длины ОМ.
Объяснение:
Прямая АВ , проходящая через начало координат имеет вид у=кх
Найдем точки пересечения этой прямой и гипербол:
y =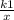
и у=кх → 
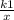= кх , х²= 
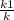; x =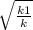 
( т.к. точка пересечения в 1 четверти , то х>0 ). Тогда у= к* 
.
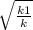y =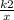
и у=кх → 
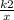= кх , х²= 
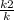; x =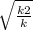 
( т.к. точка пересечения в 1 четверти , то х>0 ). Тогда у= к* 
.
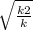По свойство касательной и секущей проведенных из одной точки ОМ²=ОА*ОВ. Найдем ОА и ОВ по формулам расстояния между точками : ОА=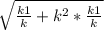
= 
,
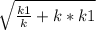ОB=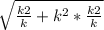
= 
.
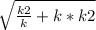Тогда ОМ²=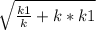
* 
= 
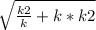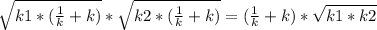. Т.к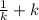 
≥2 ,по следствию из неравенства о среднем арифметическом и среднем геометрическом , то принимает наименьшее значение равное 2 , а к1*к2=144, то ОМ²=2*√144=2*12=24.
===========================================
Свойство касательной и секущей проведенных из одной точки : "Если из точки к окружности проведены касательная и секущая, то квадрат отрезка касательной от данной точки до точки касания равен произведению длин отрезков секущей от данной точки до точек её пересечения с окружностью."
Формула расстояния между точками d=√( (х₁-х₂)²+(у₁-у₂)² ), где (х₁;у₁ ), (х₂;у₂ ) -координаты концов отрезка.
Расстояние от прямой DC до плоскости α - это перпендикуляр из любой точки этой прямой на плоскость α.
Итак, в прямоугольном треугольнике АЕD катет АЕ равен по Пифагору
АЕ=√(AD²-DE²)=√(36²-18²)=18√3.
Угол между двумя пересекающимися плоскостями равен углу между прямыми, по которым они пересекаются с любой плоскостью, перпендикулярной их линии пересечения. То есть угол между плоскостью α и плоскостью квадрата - это угол EAD, cинус которого равен отношению противолежащего катета к гипотенузе: Sinβ=ED/AD=18/36=1/2. Значит угол между плоскостями равен 30°.
Площадь проекции квадрата на плоскость α - это площадь прямоугольника AEFB, равная S=AB*AE=36*18√3=648√3см²