Дан треугольник , стороны которого равны 9,8 см, 10 см, 10,2 см. Может ли он быть ортогональной проекции на некоторую плоскость треугольника , имеющего плоскость 45 см^2? ответ развернутый
В треугольнике ABC AB=√21, BC=3√21. Биссектриса внешнего угла треугольника при вершине B пересекает прямую AC в точке P, угол APB равен 30°. Найдите BP.
Внешний угол треугольника равен сумме двух других не смежных с ним.
Пусть ∠CAB = y; ∠BCA = x.
Тогда внешний угол при вершине B равен x+y.
Биссектриса делит угол пополам, поэтому ∠ABP =
По свойству внешнего угла из ΔAPB имеем:
∠CAB = ∠APB+∠ABP;
y = 30°+
2y = 60°+x+y;
y = 60°+x = ∠CAB.
В ΔABC, по теореме синусов, получим равенство:
3√(21)·sin(x) = √(21)·sin(60°+x);
3sin(x) = sin(60°)·cos(x)+cos(60°)·sin(x);
3sin(x) = ·cos(x)+ ·sin(x);
6sin(x)-sin(x) = 5sin(x) = √(3)·cos(x);
Если cos x = 0, то sin x = 0, но синус и косинус не могут одновременно равняться нулю, тогда поделим на cos x ≠ 0;
tg(x) = .
Найдём sin(x):
По основному тригонометрическому тождеству:
sin(x) = +√(3/28) т.к. 0 < x < 180°, как угол треугольника.
Правильное условие:
В треугольнике ABC AB=√21, BC=3√21. Биссектриса внешнего угла треугольника при вершине B пересекает прямую AC в точке P, угол APB равен 30°. Найдите BP.
Внешний угол треугольника равен сумме двух других не смежных с ним.
Пусть ∠CAB = y; ∠BCA = x.
Тогда внешний угол при вершине B равен x+y.
Биссектриса делит угол пополам, поэтому ∠ABP =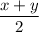
По свойству внешнего угла из ΔAPB имеем:
∠CAB = ∠APB+∠ABP;
y = 30°+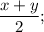
2y = 60°+x+y;
y = 60°+x = ∠CAB.
В ΔABC, по теореме синусов, получим равенство:
3√(21)·sin(x) = √(21)·sin(60°+x);
3sin(x) = sin(60°)·cos(x)+cos(60°)·sin(x);
3sin(x) =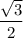
·cos(x)+
·sin(x);
6sin(x)-sin(x) = 5sin(x) = √(3)·cos(x);
Если cos x = 0, то sin x = 0, но синус и косинус не могут одновременно равняться нулю, тогда поделим на cos x ≠ 0;
tg(x) =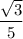
.
Найдём sin(x):
По основному тригонометрическому тождеству:
sin(x) = +√(3/28) т.к. 0 < x < 180°, как угол треугольника.
По теореме синусов в ΔCPB:
ответ: 9.
1. Дано: КМРТ - трапеция, КМ=РТ, КТ=14 дм, МР=8 дм. МН - высота, МН=4 дм. Найти КМ.
Решение: проведем высоту РС.
МР=СН=8 дм.
ΔКМН=ΔРСТ по катету и гипотенузе, КН=СТ=(14-8):2=3 дм.
Рассмотрим ΔКМН - прямоугольный, КН=3 дм, МН=4 дм, значит КМ=5 дм (египетский треугольник).
ответ: 5 дм.
2. Дано: КМСТ - прямоугольник, Р=56 см, КТ-МК=4 см. Найти МТ.
Решение: МК+КТ=56:2=28 см. Пусть КТ=х см, тогда МК=х-4 см.
Составим уравнение: х+х-4=28; 2х=32; х=16.
КТ=16 см; МК=16-4=12 см. Тогда по теореме Пифагора
МТ=√(16²+12²)=√(256+144)=√400=20 см.
(или просто: МТ=20 см, т.к. МК:КТ=12:16=3:4; МКТ - египетский треугольник)
ответ: 20 см.