Дана прямая B и точка A не принадлежащей данной прямой постройте чертеж и Найдите расстояние от данной точки до прямой

Показать ответ

Ответ:

Maryyy100

13.05.2023 10:47

обозначим вершины призмы АВСДА1В1С1Д1 с сечением АА1С1С. Объем призмы вычисляется по формуле: V=Sосн×АА1. Для этого нужно найти площадь основания и высоту призмы. Площадь ромба вычисляется по формуле: Sосн=½×АС×ВД=½×5×8=20см².

Теперь найдём высоту призмы. Сечение призмы представляет собой прямоугольник, одной из сторон которого является искомая высота АА1=СС1 площадь которого 24см², и используя формулу площади найдём высоту: AA1=S÷AC=24÷8=3см

Теперь найдём объем призмы:

V=Sосн×АА1=20×3=60см³

ОТВЕТ: V=60см³

Основанием прямой призмы является ромб, диагонали которого равны 5см и 8 см. Большее диагональное се

0,0(0 оценок)

Ответ:

serotettonika

04.04.2020 06:10

Прямая параллельная одной стороне треугольника делит его медиану проведенную к другой стороне в отношении 5:2 от вершины. В каком отношении эта прямая делит третью сторону треугольника?

Объяснение:

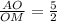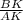Введем обозначения как показано на чертеже: КР║АС , ВМ=МС=у, МР=х . По условию $\frac{AO}{OM} =\frac{5}{2}$ . Необходимо найти $\frac{BK}{AK}$ .

Т.к. АС║КР , то по т. о пропорциональных отрезках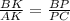 $\frac{BK}{AK} =\frac{BP}{PC}$ или

$\frac{BK}{AK} =\frac{y+x}{y-x}$ (*) . По т. Менелая для ΔВАМ :

$\frac{BK}{AK} *\frac{AO}{OM}* \frac{PM}{PB} =1$ или $\frac{BK}{AK} *\frac{5}{2}* \frac{x}{x+y} =1$ или $\frac{BK}{AK} =\frac{2}{5}* \frac{x+y}{x}$ (**).

Приравняем правые части (*) и (**) :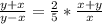 $\frac{y+x}{y-x} =\frac{2}{5}* \frac{x+y}{x}$ или 2(у-х)=5х или

$\frac{y}{x} =\frac{7}{2}$ .

Вернемся к (**)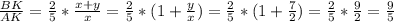 $\frac{BK}{AK} =\frac{2}{5}*\frac{x+y}{x}=\frac{2}{5}*(1+\frac{y}{x} )=\frac{2}{5}*(1+\frac{7}{2} )=\frac{2}{5}*\frac{9}{2} =\frac{9}{5}$ .