1.
Катеты фиолетового треугольника: 16; 6
Гипотенуза равна:
Гипотенуза фиолетового треугольника равна: 17.1.
2.
Чтобы найти наибольший катет бледно-красного, вычтим те 4 сантиметра с нашей гипотенузы: 17.1-4 = 13.1
Теперь к этому числу добавим те 9 сантиметров (в правой нижней стороне красного треугольника): 13.1+9 = 22.1
Теперь нам известно 2 катета бледно-красного треугольника: 22.1; 7.
Гипотенуза её равна:
Вычтим с этого числа те 2 сантиметров(в правом верхнем углу бледно-красного треугольника): 23.18-2 = 21.18.
3.
Теперь нам известна гипотенуза жёлтого треугольника, и его катет.
Второй катет равен:
Теперь мы знаем 2 катета, и гипотенузу желтого треугольника.
4.
Прибавим к наибольшому катету 5 и 1(в правом и левом нижнем углу синего треугольника): 20.3+6 = 26.3.
Теперь нам известно 2 катета синего треугольника: 12; 26.3.
Гипотенуза равна: .
5.
Вычтим 11 сантиметров с гипотенузы синего треугольника (левый нижний угол зелёного треугольника): 28.9-11 = 17.9.
Теперь нам известно 2 катета зелёного треугольника: 14; 17.9.
6.
Нам известна гипотенуза, и один катет розового треугольника: 16; 22.72.
Второй катет равен: .
7. Прибавим к этому числу 5 сантиметров (нижний левый угол голубого треугольника): 16.13+5 = 21.13.
Теперь нам известно 2 катета: 5; 21.13
Найдём гипотенузу:
Вывод: самая верхняя гипотенуза равна 21,71 сантиметров.
S = 10,08 ед.изм2
или
S = 10 8/100 ед.изм2 (десять целых восемь сотых единиц измерения в квадрате)
Объяснение:
1). Данную трапецию разделим на 3 сегмента:
1 Прямоугольник и 2 боковых треугольника.
2). Найдем площади данных фигур: (в клетках)
а). Sпр = 6 * 7 = 42 кл2.
б). Sтр1 = 5 * 6 / 2 = 15 кл2.
в). Sтр2 = 2 * 6 / 2 = 6 кл2.
Сумма данных сегментов будет являться площадью трапеции (в клетках):
г). Sтр = 42 + 15 + 6 = 63 кл2.
Единицы измерения не указаны, возможно см2, но продолжим так, зная размер клетки, получим площадь в ед.изм.:
S = 0,4 * 0,4 * 63 = 0,16 * 63 = 10,08 ед.изм2.
S = 4/10 * 4/10 * 63 = (4 * 4)/(10 * 10) * 63 = 16/100 * 63 = (16 * 63)/(100 * 1) = 1008/100 = 10 8/100 ед.изм2 (десять целых восемь сотых единиц измерения в квадрате)
1.
Катеты фиолетового треугольника: 16; 6
Гипотенуза равна: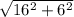
Гипотенуза фиолетового треугольника равна: 17.1.
2.
Чтобы найти наибольший катет бледно-красного, вычтим те 4 сантиметра с нашей гипотенузы: 17.1-4 = 13.1
Теперь к этому числу добавим те 9 сантиметров (в правой нижней стороне красного треугольника): 13.1+9 = 22.1
Теперь нам известно 2 катета бледно-красного треугольника: 22.1; 7.
Гипотенуза её равна:
Вычтим с этого числа те 2 сантиметров(в правом верхнем углу бледно-красного треугольника): 23.18-2 = 21.18.
3.
Теперь нам известна гипотенуза жёлтого треугольника, и его катет.
Второй катет равен: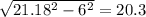
Теперь мы знаем 2 катета, и гипотенузу желтого треугольника.
4.
Прибавим к наибольшому катету 5 и 1(в правом и левом нижнем углу синего треугольника): 20.3+6 = 26.3.
Теперь нам известно 2 катета синего треугольника: 12; 26.3.
Гипотенуза равна: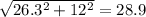 .
.
5.
Вычтим 11 сантиметров с гипотенузы синего треугольника (левый нижний угол зелёного треугольника): 28.9-11 = 17.9.
Теперь нам известно 2 катета зелёного треугольника: 14; 17.9.
Гипотенуза равна: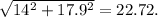
6.
Нам известна гипотенуза, и один катет розового треугольника: 16; 22.72.
Второй катет равен: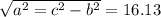 .
.
7. Прибавим к этому числу 5 сантиметров (нижний левый угол голубого треугольника): 16.13+5 = 21.13.
Теперь нам известно 2 катета: 5; 21.13
Найдём гипотенузу: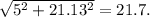
Вывод: самая верхняя гипотенуза равна 21,71 сантиметров.
S = 10,08 ед.изм2
или
S = 10 8/100 ед.изм2 (десять целых восемь сотых единиц измерения в квадрате)
Объяснение:
1). Данную трапецию разделим на 3 сегмента:
1 Прямоугольник и 2 боковых треугольника.
2). Найдем площади данных фигур: (в клетках)
а). Sпр = 6 * 7 = 42 кл2.
б). Sтр1 = 5 * 6 / 2 = 15 кл2.
в). Sтр2 = 2 * 6 / 2 = 6 кл2.
Сумма данных сегментов будет являться площадью трапеции (в клетках):
г). Sтр = 42 + 15 + 6 = 63 кл2.
Единицы измерения не указаны, возможно см2, но продолжим так, зная размер клетки, получим площадь в ед.изм.:
S = 0,4 * 0,4 * 63 = 0,16 * 63 = 10,08 ед.изм2.
или
S = 4/10 * 4/10 * 63 = (4 * 4)/(10 * 10) * 63 = 16/100 * 63 = (16 * 63)/(100 * 1) = 1008/100 = 10 8/100 ед.изм2 (десять целых восемь сотых единиц измерения в квадрате)