ΔTRS- равнобедренный, так как RТ=ТS, а высота, проведённая к основанию равнобедренного треугольника является его медианой, следовательно RЕ=ЕS=RS:2=24:2=12(см)
ΔTЕS- прямоугольный, следовательно по теореме Пифагора
TS²=ТЕ²+ЕS²=8²+12²=64+144=208
(см),
RT²=208
По теореме косинусов в ΔTRS
TS²= RТ² +RS² -2TR*RS* соs∠ R ;
2RТ*RS соs∠ R = RТ² +RS²- TS²; ( так как RТ=ТS, то RТ²-ТS²=0)
Объем - это площадь основания на высоту. Площадь основания есть площадь ромба, а высоту можешь найти исходя из того, что диагональные сечения есть прямоугольники, ширина обеих - высота, а длины равны длинам соответствующих диагоналей. Произведение диагоналей находишь из определения площади ромба. S= произведение диагоналей делённое пополам, то есть ab/2. Отсюда ab=60. Это же произведение можно ещё представить, как (96/h) *(40\h) = 3840/(h^2), где h - высота
ответ: TS=4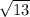
ΔTRS- равнобедренный, так как RТ=ТS, а высота, проведённая к основанию равнобедренного треугольника является его медианой, следовательно RЕ=ЕS=RS:2=24:2=12(см)
ΔTЕS- прямоугольный, следовательно по теореме Пифагора
TS²=ТЕ²+ЕS²=8²+12²=64+144=208
RT²=208
По теореме косинусов в ΔTRS
TS²= RТ² +RS² -2TR*RS* соs∠ R ;
2RТ*RS соs∠ R = RТ² +RS²- TS²; ( так как RТ=ТS, то RТ²-ТS²=0)
2RT*RS *соs ∠R =RS²;
RT*RS соs ∠R =RS²/2
В ΔRKS : RK=RT/2.
По теореме косинусов
SK²=RK²+RS²-2RK*RS*cos∠R=(RT/2)²+RS²-2(RT/2)*RS* соs ∠R=
=TR²/4+RS²- RT*RS* соs ∠R =TR²/4+RS² - RS²/2=
3840/h^2 = 60, откуда h^2 = 64, откуда h=8.
Объем равен 30*8 = 240