Дано прямокутну трапецію, менша основа якої дорівнює 4 см. Менша бічна сторона дорівнює 4 см, а більша бічна сторона утворює з основою ∠45°.
Знайди площу трапеції.

Показать ответ

Ответ:

kamil228337

23.04.2023 14:00

В прямоугольном треугольнике найти все линейные элементы

Объяснение:

ΔKNT подобен ΔMKT по 2-м углам: ∠МТК=NTK=90, ∠M=∠TKN.

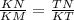Значит сходственные стороны пропорциональны : $\frac{KN}{KM} =\frac{TN}{KT}$ .

Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой ⇒ КТ=√( МТ*ТN) .

$\frac{6}{5} =\frac{TN}{\sqrt{MT*TN} }$ , $\frac{6}{5} =\frac{TN}{\sqrt{MT}*\sqrt{TN} }$ , $\frac{6}{5} =\frac{\sqrt{TN} }{\sqrt{MT} }$ , $\frac{36}{25} =\frac{TN}{TM}$ .

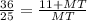Из условия TN=11+MT , поэтому $\frac{36}{25} =\frac{11+MT}{MT}$ , 36MT=25(11+MT) , MT=25. Тогда TN=11+25=36 , гипотенуза MN=25+61=61.

Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и проекций катетов на гипотенузу :

а) катет МК=√(МN*MT) , MK=√(25*61)=5√61;

б) катет КN=√(МN*TN) , KN=√(36*61)=6√61.

в) высота КТ=√( МТ*ТN) , КТ=√( 25*36)=30 .

с задачей. Найдите все линейные элементы , угол К = 90°.

0,0(0 оценок)

Ответ:

alenaefremova79

11.08.2022 05:12

10,7π - 16√3

Объяснение:

S= Sсектора - Sт

Sсектора = Sкруга/360х60

Sкр=πR∧2=π8∧2=64π

Sсектора = 64п/360х60= 10,7π

Треугольник является равносторонним, поскольку образован радиусами (значит, МО=МН), центральный угол по условию равен 60 градусам, значит каждый из оставшихся углов равен (180-60):2= 60 градусов

Площадь треугольника равна 1/2 х квадрат стороны х sin угла 60 градусов

Sт= 1/2 x 64 x √3/2 = 16√3

Соответственно, S = 10,7π- 16√3

Можно, конечно, все рассчитать, если требуется по условию:

10,7х3,14-16х1,73=33,6-27,68=5,92

0,0(0 оценок)

Популярные вопросы: Геометрия