Пусть О- центр окружности
AM-медиана
r=(b/2)*√(2a-b)/(2a+b))
В нашем случае
r= (16/2)*√((20-16)/(20+16))=8√(4/36)=8*(1/3)=8/3
Пусть AM=x, тогда OM=x/3
то есть AM=8
Откуда
AO=8-8/3=16/3
Треугольники AOM и AMB - подобны Из подобия треугольников
BM/MO = AM/AO => MO=BM*AO/AM=(8*16/3)/8=16/3
MT=2BM=32/3
MT-диаметр.
Диаметр- 2 радиуса
Центр вписанной окружности-точка пересечения биссектрис.
Биссектриса угла лежащего против основания является так же высотой.
высота=
точкой пересечения биссектрис данная биссектриса, она же высота, делится на 2 части с отношением 2/1
радиус =6/3=2
Диаметр=2*2=4
ответ: MT=4
Пусть О- центр окружности
AM-медиана
r=(b/2)*√(2a-b)/(2a+b))
В нашем случае
r= (16/2)*√((20-16)/(20+16))=8√(4/36)=8*(1/3)=8/3
Пусть AM=x, тогда OM=x/3
то есть AM=8
Откуда
AO=8-8/3=16/3
Треугольники AOM и AMB - подобны Из подобия треугольников
BM/MO = AM/AO => MO=BM*AO/AM=(8*16/3)/8=16/3
MT=2BM=32/3
MT-диаметр.
Диаметр- 2 радиуса
Центр вписанной окружности-точка пересечения биссектрис.
Биссектриса угла лежащего против основания является так же высотой.
высота=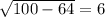
точкой пересечения биссектрис данная биссектриса, она же высота, делится на 2 части с отношением 2/1
радиус =6/3=2
Диаметр=2*2=4
ответ: MT=4