Даны два прямоугольника параллелепипеда: ребра одного равны а , b и b, а ребра другого равны а , а и b/ НА сколько площадь полной поверхности первого параллелепипеда больше , чем площадь поверхности второго параллелепипеда если а= 1000 b = 1001
Сириус курсы. Геометрия. 9 класс. v1.4. Радикальные оси. Задача №5.
1. Чертим 2 пересекающиеся прямые. Т.к прямые бесконечны, то их можно чертить в любых масштабах. Начертим , маленькие.
2.Отмечаем точки на них, подписываем цифрами длину отрезков.
3. Как известно из видео, которое ты невнимательно смотрела, длины если произведения отрезков, находящихся на одной прямой и имеющих общую точку соответственно равно произведению отрезков, находящихся на второй прямой, то эти отрезки лежат на одной окружности, а значит и точки, которыми соединяются отрезки лежат на этой окружности.
4. Перебираем варианты: ( О - общая точка пересечения нужных отрезков)
1. AO*OB = OD* OE
2. AO*OC = OG*OD
Следовательно подходят варианты:
ADBE, ADCG.
P.S. Курсы созданы, чтобы там стараться и додумывать самим)
В прямоугольном треугольнике найти все линейные элементы
Объяснение:
ΔKNT подобен ΔMKT по 2-м углам: ∠МТК=NTK=90, ∠M=∠TKN.
Значит сходственные стороны пропорциональны : .
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой ⇒ КТ=√( МТ*ТN) .
, , , .
Из условия TN=11+MT , поэтому , 36MT=25(11+MT) , MT=25. Тогда TN=11+25=36 , гипотенуза MN=25+61=61.
Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и проекций катетов на гипотенузу :
ADBE, ADCG
Объяснение:
Сириус курсы. Геометрия. 9 класс. v1.4. Радикальные оси. Задача №5.
1. Чертим 2 пересекающиеся прямые. Т.к прямые бесконечны, то их можно чертить в любых масштабах. Начертим , маленькие.
2.Отмечаем точки на них, подписываем цифрами длину отрезков.
3. Как известно из видео, которое ты невнимательно смотрела, длины если произведения отрезков, находящихся на одной прямой и имеющих общую точку соответственно равно произведению отрезков, находящихся на второй прямой, то эти отрезки лежат на одной окружности, а значит и точки, которыми соединяются отрезки лежат на этой окружности.
4. Перебираем варианты: ( О - общая точка пересечения нужных отрезков)
1. AO*OB = OD* OE
2. AO*OC = OG*OD
Следовательно подходят варианты:
ADBE, ADCG.
P.S. Курсы созданы, чтобы там стараться и додумывать самим)
В прямоугольном треугольнике найти все линейные элементы
Объяснение:
ΔKNT подобен ΔMKT по 2-м углам: ∠МТК=NTK=90, ∠M=∠TKN.
Значит сходственные стороны пропорциональны :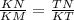 .
.
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой ⇒ КТ=√( МТ*ТN) .
Из условия TN=11+MT , поэтому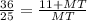 , 36MT=25(11+MT) , MT=25. Тогда TN=11+25=36 , гипотенуза MN=25+61=61.
, 36MT=25(11+MT) , MT=25. Тогда TN=11+25=36 , гипотенуза MN=25+61=61.
Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и проекций катетов на гипотенузу :
а) катет МК=√(МN*MT) , MK=√(25*61)=5√61;
б) катет КN=√(МN*TN) , KN=√(36*61)=6√61.
в) высота КТ=√( МТ*ТN) , КТ=√( 25*36)=30 .