Даны точки A(6;6) и B(8;12). Найди координаты точек C и D, если известно, что точка B — середина отрезка AC, а точка D — середина отрезка BC.
С ( )
D ( )

Пусть Х градусов приходится на 1 часть ,
тогда 2х - приходятся на 2 части
5х- приходятся на 5 частей
Т к треугольник тупоугольный , то 5х - это величина тупого угла
2х- это величина угла при основании и таких углов два, т к треугольник равнобедренный , а в равнобедренном треугольнике углы при основании равны
Известно, что сумма внутренних углов треугольника равна 180 град
Составим уравнение :
2х+2х+5х=180
9х=180
Х=20 град - приходится на1 часть
2х=20*2=40 град - величина углов при основании
5х=20*5=100 град - величина тупого угла
ответ: 40 град
40 град
100 град

Из точки А проведены две секущие  АВ и АС, которые пересекают  окружность в точках К и М так, что AB = 2 см, ВС = 4 см,  AC = 5 см, AK = 1 см. Найдите МК​.

Объяснение:

1)∠AKM =180°-∠BKM по т. о смежных углах ; ∠C=180°-∠BKM по  свойству углов вписанного 4-х угольника   ⇒ ∠AKM =∠C.

2) ΔAKM ~ΔACB по двум углам : ∠A_общий , ∠AKM =∠C.

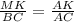Сходственные стороны в подобных треугольниках пропорциональны : ,    ⇒ MK=(1*4):5=0,8 (см)

============================

Свойство углов вписанного 4-х угольника

Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180°.