3) Необходимо поставь точку, это будет вершина, основание проведи, к нему перпендикуляр, но так, что бы он был по центру основания, останется провести боковые стороны) (если вершина А, то должно быть: сторона АВ=АС)
2) Пусть дан треугольник АВС, угол С=90⁰, из угла С проведена бисектриса СD,углы АСD и ВСD равны по 45⁰, тогда по условию угол АDС=70⁰. Найдем угол DАС из треугольника DАС. По теореме о сумме углов треугольника: уголDАС=180⁰-(45⁰+70⁰)=65⁰. Из треугольника АВС: Угол АВС= 90⁰-65⁰=25⁰.
ответ:25⁰, 65⁰
1) угол ВАС=180-90-60=30
Т.к. сторона, лежащая против угла в 30 равна половине гипотенузы, то ВВ1=1/2АВ
Объяснение:
3) Необходимо поставь точку, это будет вершина, основание проведи, к нему перпендикуляр, но так, что бы он был по центру основания, останется провести боковые стороны) (если вершина А, то должно быть: сторона АВ=АС)
2) Пусть дан треугольник АВС, угол С=90⁰, из угла С проведена бисектриса СD,углы АСD и ВСD равны по 45⁰, тогда по условию угол АDС=70⁰. Найдем угол DАС из треугольника DАС. По теореме о сумме углов треугольника: уголDАС=180⁰-(45⁰+70⁰)=65⁰. Из треугольника АВС: Угол АВС= 90⁰-65⁰=25⁰.
ответ:25⁰, 65⁰
1) угол ВАС=180-90-60=30
Т.к. сторона, лежащая против угла в 30 равна половине гипотенузы, то ВВ1=1/2АВ
т.к ВВ1=8см
то АВ=2*8=16 см
ответ: 16 см
а) ∠В = 30°, АВ=4 см, AD=ВD=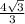
см ∠D=120°
б) S = 2√3 cм²
Объяснение:
а) Сумма острых углов прямоугольного треугольника равна 90°
∠В=90°-∠А=90°-60°=30°
Катет прямоугольного треугольника, лежащий напротив угла в 30° равен половине гипотенузы.
⇒ АВ=2*АС=2*2=4см
По теореме Пифагора найдём катет ВС:
ВС = 2√3 см
Биссектриса угла треугольника делит противолежащую сторону в отношении длин прилежащих сторон.Рассмотрим ΔABD: ∠ВАD=30° - так как AD – биссектриса, ∠В=30° ⇒ ΔABD- равнобедренный, AD=ВD=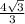
см
Так как сумма углов треугольника = 180°, то
∠АDB = 180-∠ВАD-∠В=180-30-30=120°
б) Площадь прямоугольного треугольника равна произведению двух его катетов деленное на 2:
S = 2√3 cм²