В линейной функции y = kx+b
k и b — числовые коэффициенты.
Графиком является прямая.
k – "направление" по оси X
b – смещение по оси Y
Если k>0, то прямая будет идти в "положительную" сторону по оси X,
если k<0, то прямая бужет идти в "минус" по оси X.
(прямая, образно, идёт снизу вверх)
/рис. 1/
График функции, прямая, пересекается с осью Y в точке b
/рис. 2/
Смотрим "направление" функции:
в первом графике k>0,
во втором графике k<0,
в третьем графике k<0.
Смотрим пересечение функции с осью Y:
В первом графике b>0,
во втором графике b<0,
в третьем графике b>0.
1 — В, 2 — А, 3 — Б
Найдите отношение объёма октаэдра к объёму куба, вершинами которого являются центры граней октаэдра.
Объяснение:
1) Октаэдр это геометрическое тело из восьми граней, каждая их которых - правильный треугольник. Пусть ребро октаэдра а.
V( октаэдра)=1/3*√2*а³ , ABCD-квадрат .
2) Пусть Р-центр правильного ΔАВМ .Тогда М-точка пересечения медиан .Тогда по т. о точке пересечения медиан ⇒ .
3) Аналогично для правильного ΔDCМ ⇒ .
4) ΔМРК подобен ΔМXY по 2-м пропорциональным сторонам ( см п. 2,3) и равному углу между этими сторонами (∠РМК-общий).
Тогда , ,РК= *а .
5) V( куба)=( *а)³ = *а³ . Тогда отношение объёмов будет равно :
= .
В линейной функции y = kx+b
k и b — числовые коэффициенты.
Графиком является прямая.
k – "направление" по оси X
b – смещение по оси Y
Если k>0, то прямая будет идти в "положительную" сторону по оси X,
если k<0, то прямая бужет идти в "минус" по оси X.
(прямая, образно, идёт снизу вверх)
/рис. 1/
График функции, прямая, пересекается с осью Y в точке b
/рис. 2/
Смотрим "направление" функции:
в первом графике k>0,
во втором графике k<0,
в третьем графике k<0.
Смотрим пересечение функции с осью Y:
В первом графике b>0,
во втором графике b<0,
в третьем графике b>0.
1 — В, 2 — А, 3 — Б
Найдите отношение объёма октаэдра к объёму куба, вершинами которого являются центры граней октаэдра.
Объяснение:
1) Октаэдр это геометрическое тело из восьми граней, каждая их которых - правильный треугольник. Пусть ребро октаэдра а.
V( октаэдра)=1/3*√2*а³ , ABCD-квадрат .
2) Пусть Р-центр правильного ΔАВМ .Тогда М-точка пересечения медиан .Тогда по т. о точке пересечения медиан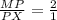 ⇒
⇒ 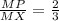 .
.
3) Аналогично для правильного ΔDCМ ⇒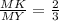 .
.
4) ΔМРК подобен ΔМXY по 2-м пропорциональным сторонам ( см п. 2,3) и равному углу между этими сторонами (∠РМК-общий).
Тогда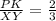 ,
, 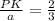 ,РК=
,РК= 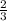 *а .
*а .
5) V( куба)=(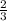 *а)³ =
*а)³ = 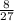 *а³ . Тогда отношение объёмов будет равно :
*а³ . Тогда отношение объёмов будет равно :